Метод множителей Лагранжа

Если нужно найти экстремум (максимум, минимум или седловую точку) функции n переменных f(x₁, x₂, …, x_n), связанных k<n условиями зависимости, которые могут быть записаны в виде u_i(x₁, x₂, …, x_n)=0, при i=1,2,…k, то вводят k неопределенных множителей l_i и рассматривают новую функцию Ф(x₁, x₂, …, x_n, l₁, l₂, …, l_k) n+k аргументов:

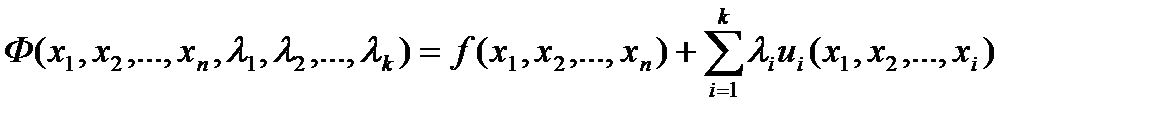Значения аргументов, при которых достигается экстремум, находится путём решения системы из n+k уравнений:

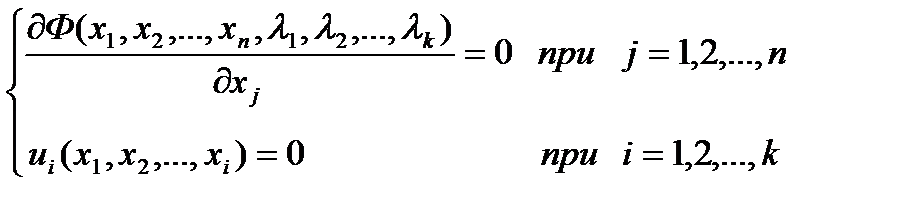
Для определения того, какой из эстремумов найден (максимум, минимум или седловая точка) проверяются знаки вторых производных функции Ф по всем аргументам x в точке экстремума. Если все эти производные положительны, найден минимум, отрицательны – максимум, знаки разные – седловая точка.

Используем теперь метод множителей Лагранжа для определения значений вероятностей, при которых энтропия максимальна.

Значит, следует найти максимум функции 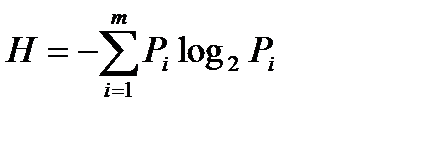при условии .

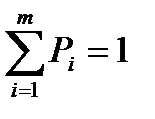Согласно методу Лагранжа все k условий (оно у нас сейчас одно, т.е. k=1) нужно привести к виду: u_i(x₁, x₂, …, x_n)=0, при i=1,2,…k. В нашем конкретном случае получаем: .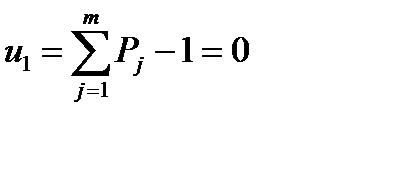

Образуем вспомогательную функцию

.

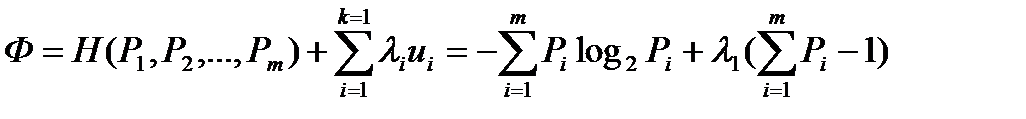Составляем и преобразуем систему уравнений:

Учтем, что: .

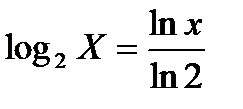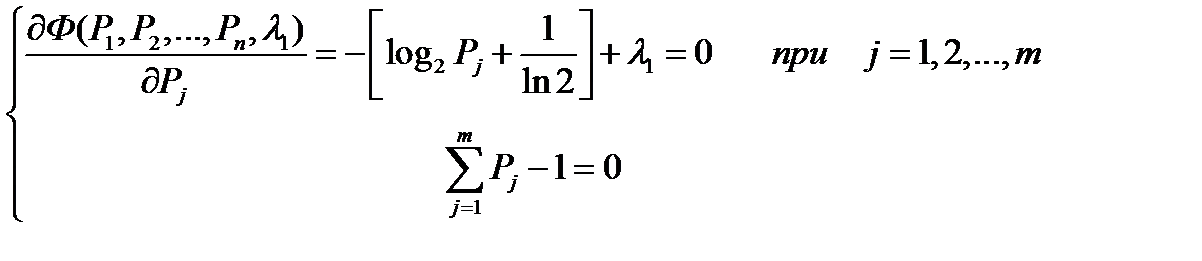
Из верхних уравнений находим, что 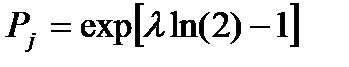, т.е. все P_j равны между собой и значит, как следует из нижнего уравнения, равны 1/m .

Надо теперь выяснить, какой вид экстремума нами найден. Для этого проанализируем знаки второй производной функции Ф:

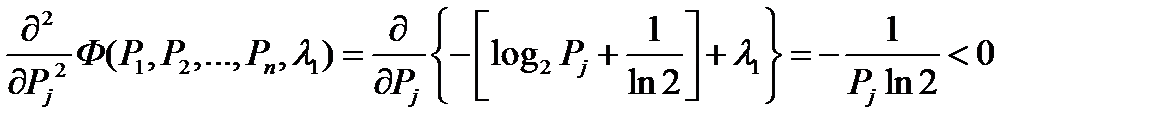, т.к. P_j>0 и ln2>0 .

Следовательно, нами найдет именно максимум. Значит, энтропия источника максимальна тогда, когда все выдаваемые им сообщения равновероятны, а формула количества получаемой при этом информации совпадает с формулой количества информации по Хартли.