Энтропия и средняя энтропия простого события

Рассмотрим подробнее понятие энтропии[1] в разных вариантах, так как оно используется в шенноновской теории информации. Энтропия - мера неопределенности некоторого опыта. В простейшем случае его исход зависит от выбора одного элемента из множества исходных. Множество исходных элементов называется выборочным пространством. Совокупность событий, состоящих в выборе различных элементов из выборочного пространства, называется полной группой событий.

Вероятности событий ─ положительные числа со значениями, принадлежащими интервалу [0,1], а их сумма равна 1. Выборочное пространство и его вероятностные характеристики в совокупности представляют собой ансамбль сообщений. Допустим, имеется полная группа событий, заключающихся в получении одного из множества сообщений: а₁, а₂, ..., а_m.

Обозначим вероятности появления сообщений: P₁, P₂, ..., P_m.

В этом случае энтропия конкретного k-го сообщения равна:

H_k = - log₂(P_k) .

Чаще, однако, используют усредненную по всем возможным сообщениям энтропию, которая в данном случае, если сообщения получаются от источника сообщений, называется энтропией источника сообщений.

Как известно из курсов теории вероятностей и математической статистики, среднее значение дискретно распределенной случайной величины Х, независимо принимающей значения из ряда Х₁, Х₂, ..., Х_m с вероятностями P₁, P₂, ..., P_m, равно: .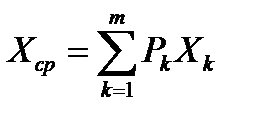

Используя эту формулу для усреднения энтропии Н_k, получим:

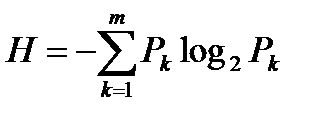
Здесь Н является средней неопределенностью, приходящейся наодно сообщение, т.е. энтропией источника сообщений.

Исследуем эту формулу подробнее. Предположим, что сообщения равновероятны. Тогда P_k = 1/m .

Подставив эту вероятность в формулу энтропии источника, получим:

.

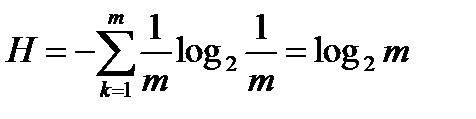Заметим, что эта формула совпадает с выражением для количества информации по Хартли. Таким образом, количество информации по Хартли можно считать частным случаем количества информации по Шеннону, когда события равновероятны.

Исследуем теперь область значений, которые может принимать энтропия.

Поскольку вероятность P_k лежит в интервале от 0 до 1, слагаемые в формуле энтропии всегда либо отрицательны, либо равны 0. Последнее получается, если либо P_k=1, либо P_k=0 (в этом случае получается неопределенность типа 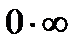, которую можно разрешить с помощью правила Лопиталя[2]). Поэтому энтропия Н может быть только положительной или равной 0.

Найдем теперь, при каком наборе вероятностей Р_k энтропия Н максимальна (ее минимум =0). Это задача на условный экстремум функции многих вещественных аргументов.

Таким образом, ищется максимум функции:

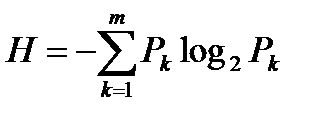при условии, что .

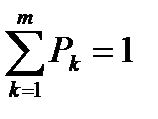Это задача на поиск условного экстремума (максимума, минимума или седловой точки). Для решения таких задач удобно использовать метод Лагранжа, называемый еще методом множителей Лагранжа. Далее он будет часто использоваться, поэтому опишем без доказательства[3] его суть (вообще-то его должны были рассматривать в курсе математики).