Анализ сетевого графика
1. Наиболее раннее возможное время наступления j-ого события Tp(j)
где символами
- i и jобозначаются номера предшествующего и последующего событий соответственно;
-tij — продолжительность (i, j) -й работы.
Из обозначения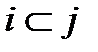 следует, что событие i предшествует событию j.
следует, что событие i предшествует событию j.
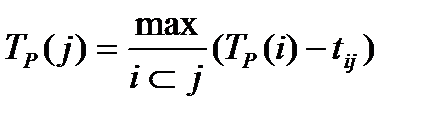
2. Самое позднее допустимое время наступления i-го события Тп (i), вычисляемое по формуле
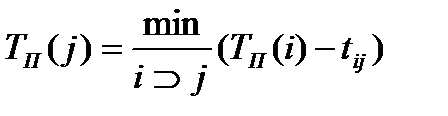
где из обозначения  следует, что событие j предшествует событию i
следует, что событие j предшествует событию i
3. Резерв времени данного события Ri вычисляемый по формуле
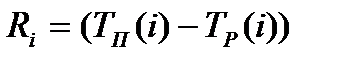
| № | Tp(j) | Tп(j) | Ri |
4. Полный резерв времени работы rп (i,j), вычисляемый по формуле
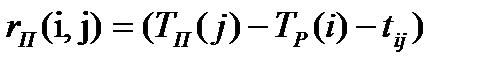
Смысл полного резерва времени работы заключается в том, что задержка в выполнении работы (i,j) на величину ∆t ij ≥ rп (i,j), приводит к задержке в наступлении завершающего события на величину (∆t ij - rп (i,j)).
5. Свободный резерв времени работы rc (i,j), вычисляемый по формуле
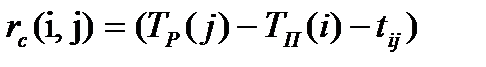
Смысл свободного резерва времени работы заключается в том, что задержка в выполнении работы на величину∆t ij≤rC(i,j), не влияет ни на один другой срок, определенный данным сетевым графиком.
| № | rп(ij) | rc(ij) |
| (0,1) | ||
| (1,2) | ||
| (2,3) | ||
| (3,4) | -10 | |
| (4,17) | ||
| (1,5) | -5 | |
| (5,6) | -5 | |
| (6,7) | -5 | |
| (7,17) | ||
| (1,8) | -5 | |
| (8,9) | -7 | |
| (9,10) | -7 | |
| (10,11) | -7 | |
| (11,17) | ||
| (0,12) | ||
| (12,13) | ||
| (13,14) | ||
| (14,15) | ||
| (15,16) | ||
| (16,17) | ||
| (11,13) | -8 | -3 |
| (17,18) |
1) Расчет критического пути:
Критический путь — это полный путь, на котором суммарная продолжительность работ является максимальной. Иными словами, это самый длинный по времени путь в сетевом графике от исходного до завершающего события. Критический путь лимитирует выполнение операции, поэтому любая задержка на работах критического пути увеличивает время всего процесса. События, через которые проходит критический путь, и работы, лежащие на критических путях, называются напряженными. У критических работ как полные, так и свободные резервы времени равны нулю (признак критической работы). Критический путь рассчитывается путем определения работ, полные резервы времени которых равны нулю.
а0 → а12 →а13 →а14 → а15 →а16 → а17 → а18
Tкп = t0,12 + t12,13 + t13,14 + t14,15 + t15,16 + t16,17 + t17,18 =27
2) Расчет полного резерва времени ненапряженного пути:
а0 →а1 → а2 → а3 → а4 →а17 → а18
Tпрв = t0,1 + t1,2 + t2,3 + t3,4 + t4,17 + t17,18 =17
Полный резерв времени ненапряженного пути — это резерв времени ненапряженных событий и работ, т. е. тех, которые лежат не на критическом пути. В том случае, если ненапряженный и критический пути не пересекаются, полный резерв времени ненапряженного пути равен разности между его длиной и длиной критического пути (во временной мере). Если ненапряженный и критический пути пересекаются, полный резерв времени равен самому длительному участку ненапряженного пути, заключенному между соответствующими парами событий критического пути. Полный резерв времени ненапряженного пути показывает, на сколько в сумме может быть увеличена продолжительность всех работ этого пути без изменения срока выполнения операции в целом.
Сущность анализа сетевого графика заключается в том, что выявляются резервы времени работ, лежащих на ненапряженных путях, и направляются на работы, лежащие на критическом пути, который лимитирует срок завершения работы в целом. Этим достигается сокращение времени выполнения критических работ, а значит, и всей операции.
Дата добавления: 2017-01-08; просмотров: 3697;











