Намагниченность. Магнитная восприимчивость и маг-нитная проницаемость среды.
Для количественного описания намагничивания магнетиков вво-дят векторную величину − намагниченность, которая определяется магнитным моментом единицы объема магнетика:
| J =lim | ∑ pm , | (4.2.1) | ||
| V | ||||
| V →0 | V |
где V − физически бесконечно малый объем, взятый в окрестности рассматриваемой точки.
Намагниченность принято связывать не с магнитной индукцией, а с напряженностью магнитного поля. В несильных полях намагничен-ность прямо пропорциональна напряженности поля, вызывающего
намагничивание:
(4.2.2)
где χ − характерная для каждого магнетика безразмерная величина,
называемая магнитной восприимчивостью вещества.
B0
Iмикро
Рис. 4.2.1
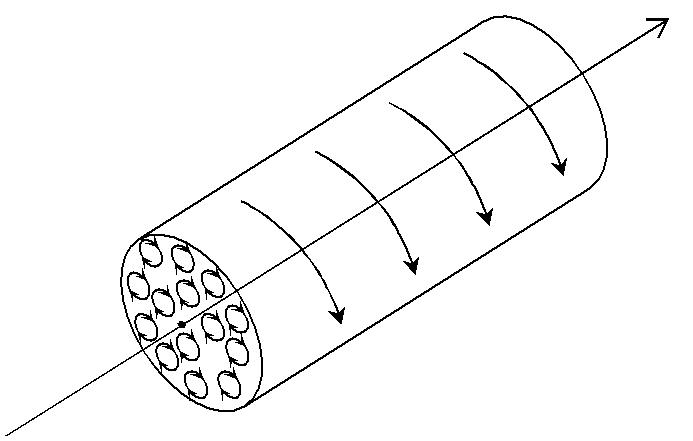
Для описания поля, создаваемого молекулярными токами, рас-смотрим магнетик в виде кругового цилиндра сечения S и длины l, внесенного в однородное внешнее магнитное поле с индукцией В0. Плоскости всех молекулярных токов располагаются перпендикулярно вектору B0 (рис. 4.2.1). Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магне-
тика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются. Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность ци-линдра ( рис. 4.2.1). Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и создает внутри него поле, магнитную ин-дукцию Bi которого можно вычислить по формуле (1.6.4) (если пред-ставить что рассматриваемый магнетик является соленоидом, состоя-щим из одного витка):
| Bi =μ0 | Iмикро | , | (4.2.3) | |
| l |
где Iмикро − сумма сил молекулярных токов, текущих по поверхности цилиндра; l − длина рассматриваемого цилиндра.
Магнитный момент этого тока
| p = I | микро | S = | I микро Sl | = | Iмикро | V , | (4.2.4) | |
| m | l | l | ||||||
где V − объем магнетика.
Намагниченность J магнетика будет равна:
J = pVm = Iмикроl .
Сопоставляя формулу (4.2.3) и (4.2.5), получим: B i =μ0J или B i =μ0J.
Подставим (4.2.6) в (4.2.1) и получим:
B = B i + B0=μ0 J + B0=μ0 J +μ0H,
с учетом (4.2.6)
(4.2.5)
(4.2.6)
(4.2.7)
B =μ0 J +μ0 H =μ0χH +μ0 H =μ0(1+χ) H =μ0μH , (4.2.8)
где 1 + χ = μ − безразмерная величина, называемая магнитной прони-цаемостью среды.Магнитная проницаемость среды показывает,восколько раз индукция магнитного поля в веществе больше индукции поля в вакууме при одной и той же его напряженности:
| μ = | B | = | B | . | ||
| μ 0 H | ||||||
| B0 | (4.2.9) |
Так как магнитная восприимчивость χ бывает как положитель-ной, так и отрицательной, то магнитная проницаемость среды μ может быть как больше, так и меньше единицы.
Лекция № 6
4.3. Типы магнетиков. Элементарная теория диа- и парамагнетизма.
4.4. Ферромагнетики. Магнитный гистерезис. Точка Кюри.
4.5. Эффекты, наблюдаемые в ферромагнетиках и их применение.
4.6. Условия для магнитного поля на границе раздела двух изо-тропных сред (для самостоятельной работы).
Дата добавления: 2017-01-08; просмотров: 1912;











