Расчет систем подчиненного регулирования

Системы подчиненного регулирования (СПР) в настоящее время получили широкое распространение из-за ряда преимуществ: простоты расчета
и наладки, легкости ограничения любой регулируемой координаты привода, возможности построения системы управления на основе унифицированных блоков УБСР – АИ.

Системы подчиненного регулирования являются многоконтурными
с каскадным включением регуляторов, количество которых соответствует числу регулируемых переменных электропривода. На входе каждого регулятора сравниваются сигналы, пропорциональные заданному и действительному значениям регулируемой координаты данного контура, а выходное напряжение регулятора служит заданием для последующего регулятора (контура).

Структурная схема двухконтурной системы подчиненного регулирования с регуляторами тока и скорости изображена на рис. 5.1, где SJ – задатчик интенсивности (либо инерционное звено для ПИ – регулятора скорости [1]). Регулятор тока выбирается обычно типа ПИ, регулятор скорости в зависимости от требуемого статизма механических характеристик может быть типа П либо ПИ [1].

Общий порядок расчета СПР следующий:

Объект регулирования представляется в виде последовательной цепочки интегральных и апериодических линейных звеньев с передаточными функциями W 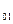(p), W 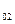(p), W 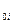(p), не имеющих между собой других связей, кроме образующих последовательную цепочку.

Рис. 5.1. Структурная схема двухконтурной системы подчиненного регулирования

Влиянием внутренних отрицательных обратных связей объекта регулирования пренебрегают или его компенсируют введением положительных обратных связей с такими же передаточными функциями.

Количество регуляторов с передаточными функциями W 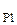(p), W 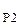(p), W 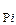(p) в системе регулирования устанавливают равным количеству контролируемых переменных. Все регуляторы соединяются между собой последовательно, так что заданием для каждого последующего регулятора является сигнал выхода предыдущего. На вход каждого регулятора подают отрицательную обратную связь по той переменной, которая регулируется данным
регулятором. Таким образом, в системе образуются охватывающие последовательно друг друга контуры регулирования от внутреннего (первого) до внешнего контура, т. е. количество контуров равно количеству регулируемых переменных.

Ограничение по величине любой из регулируемых переменных достигается ограничением сигнала с выхода предыдущего регулятора.

На выходе регулирующей части системы регулирования устанавливается фильтр, определяющий полосу пропускания и обеспечивающий тем самым помехозащищенность всей системы. Постоянная времени Т_µ этого фильтра является основным параметром системы авторегулирования и определяет ее свойства (быстродействие, точность регулирования).

Передаточные функции регуляторов W 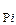(p) выбирают по методу последовательной коррекции, так чтобы получилась передаточная функция стандартного вида для замкнутого контура, то есть передаточная функция регулятора определяется структурой и параметрами соответствующего звена объекта регулирования, а также критерием оптимизации этого контура.

Получить максимальное быстродействие в замкнутом контуре – значит сделать его полностью безинерционным. Для этого в каждом контуре последовательно с объектом регулирования нужно поставить регулятор, полностью компенсирующий постоянные времени объекта регулирования, т. е. математически как бы обладающий обратной передаточной функцией:

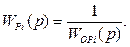(5.1)

Однако мгновенное быстродействие системы недопустимо из-за необходимого ограничения скорости нарастания тока якоря (коммутационные возможности двигателя, ударные нагрузки на механизм) и малой помехозащищенности. Таким образом, все постоянные времени объекта регулирования разбивают на «большие», действие которых должно быть скомпенсировано регулятором, и «малые», сумма которых Т 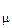не компенсируется, т. е., с одной стороны, определяется помехоустойчивость СПР, а с другой – ее максимальное быстродействие. Предполагается, что все некомпенсируемые инерционности объекта регулирования 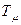заключены в первом внутреннем контуре. Исходя из требования необходимой помехозащищенности контура обычно допускается лищь однократное дифференцирование сигнала. Поэтому если в контуре регулирования переменной имеется больше двух подлежащих компенсации больших и средних постоянных времени, то прибегают к введению дополнительных подчиненных контуров регулирования.

Передаточную функцию регулятора W 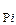(p) выбирают такой, чтобы передаточная функция замкнутого контура соответствовала требуемой стандартной. Однако для упрощения расчетов задаются желаемой передаточной функцией разомкнутого оптимизированного контура W 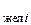(p), которая после подключения обратной связи W (p) преобразуется в передаточную функцию стандартного вида замкнутого контура. Передаточную функцию разомкнутого контура также можно записать как произведение передаточных функций отдельных звеньев

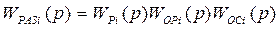. 5.2)

Учитывая, что 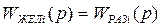, получим передаточную функцию регулятора

W 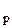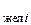(p) = W 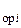(p)/ W (p) W 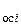(p). (5.3)

Желаемую передаточную функцию выбирают в соответствии с критерием оптимальности, определяемым требованиями к регулировочным свойствам системы электропривода. В СПР используют два критерия оптимальности: модульный и симметричный.

Желаемую передаточную функцию разомкнутого i-го контура, настроенного на модульный оптимум, в общем виде можно записать в виде

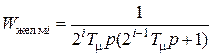, (5.4)

а для симметричного оптимума

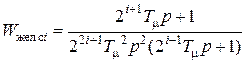. (5.5)

Тогда передаточная функция замкнутого контура, настроенного на модульный оптимум, соответствует колебательному звену второго порядка с коэффициентом затухания 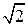/ 2 и имеет вид

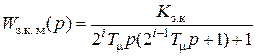, (5.6)

где 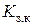– коэффициент передачи замкнутого контура. Перерегулирование выходной координаты (5.6) контура составляет примерно 4,3%, время первого достижения установившегося значения 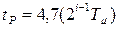, а время переходного процесса 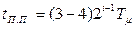. Из формулы (5.6) видно, что с увеличением номера контура i быстродействие уменьшается, так как возрастает некомпенсированная постоянная времени .

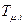Введение интегрирующего звена в передаточную функцию регулятора обеспечивает повышение точности регулирования, так как контур приобретает астатизм.

Оптимизацию системы с последовательной коррекцией начинают
с первого внутреннего контура, последовательно переходя к внешним. При переходе к внешнему контуру передаточную функцию оптимизированного внутреннего подчиненного контура упрощают, аппроксимируя ее звеном первого порядка.