Расчет параметров контура скорости
Структурная схема контура скорости приведена на рис. 5.4, где МЧ – механическая часть электропривода; КТ – контур тока; Рω – регулятор скорости.
Передаточная функция разомкнутого контура скорости (5.2) имеет вид
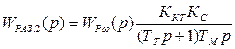 . (5.13)
. (5.13)
Желаемая передаточная функция второго (i = 2) разомкнутого контура скорости (5.4) при настройке его на модульный оптимум
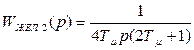 . (5.14)
. (5.14)
Тогда согласно формуле (5.3) получим передаточную функцию регулятора скорости
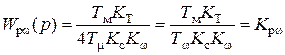 , (5.15)
, (5.15)
где Kрω – передаточная функция регулятора скорости; Тω = 2Тт = 4Т 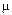 = 4Тп – постоянная времени замкнутого оптимизированного контура скорости на модульный оптимум.
= 4Тп – постоянная времени замкнутого оптимизированного контура скорости на модульный оптимум.


Рис. 5.4. Структурная схема контура скорости


Рис. 5.5. Схема П-регулятора скорости
Уравнению (5.15) соответствует пропорциональный (П) регулятор скорости (рис 5.5) с передаточным коэффициентом
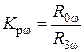 , (5.16)
, (5.16)
где R0ω = (10–100) кОм – рекомендуемые значения.
Передаточный коэффициент обратной связи по скорости:
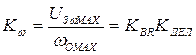 , (5.17)
, (5.17)
где KBR = UBR ном/ωBR.ном – передаточный коэффициент тахогенератора;
Kдел = R2/(R1+R2) – коэффициент передачи резисторного делителя напряжения, определяемый из условия 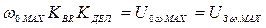 ;(R1+R2) – суммарное сопротивление делителя выбирают таким, чтобы нагрузка тахогенератора не превышала допустимую.
;(R1+R2) – суммарное сопротивление делителя выбирают таким, чтобы нагрузка тахогенератора не превышала допустимую.
Для ограничения тока якорной цепи на допустимом уровне применяют ограничение задающего сигнала Uзт на входе контура тока с помощью стабилитронов VD1 и VD2 (рис. 5.5), так как согласно формуле (5.12)
Iя мах = KктUзтмах. (5.18)
Передаточная функция замкнутого контура оптимизированного контура скорости:
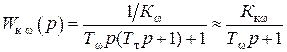 , (5.19)
, (5.19)
где Kкω = 1/Kω – коэффициент передачи замкнутого контура скорости;
Тω = 2Тт – постоянная времени контура скорости, оптимизированного на модульный оптимум.
Рассчитанная система регулирования угловой скорости двигателя является однократноинтегрирующей. Статическая точность регулирования такой системы зависит от соотношения параметров и определяется [1] выражением
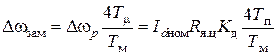 , (5.20)
, (5.20)
где Rя.ц – суммарное сопротивление якорной цепи; Тм =JΣRя.ц/(СеФ)2 – электромеханическая постоянная времени двигателя.
Относительное изменение угловой скорости двигателя в однократноинтегрирующей системе при изменении нагрузки на валу от нуля до номинального значения рассчитывается на нижней границе диапазона регулирования
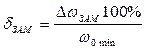 . (5.21)
. (5.21)
Однократноинтегрирующая система обеспечивает требуемые регулировочные свойства при условии
δзам ≤ δзад, (5.22)
где δзад – заданный статизм (табл. П1).
В случае невыполнения условия (5.22) для стабилизации угловой скорости вращения двигателя необходимо применять двухкратноинтегрирующую систему. В этом случае для контура скорости применяют стандартную настройку на симметричный оптимум. При такой настройке желаемую передаточную функцию разомкнутого i-го контура регулирования записывают в виде (5.5), и для второго контура (контура скорости) получают
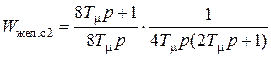 . (5.23)
. (5.23)
Тогда по формуле (5.3), учитывая формулы (5.13) и (5.23),получим передаточную функцию ПИ-регулятора скорости при настройке контура на симметричный оптимум
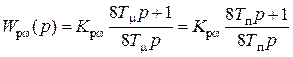 , (5.24)
, (5.24)
где Kрω = ТмKт/(ТωKсKω) – коэффициент передачи регулятора скорости, аналогичный (5.15).
Передаточная функция замкнутого контура скорости, оптимизированного на симметричный оптимум, будет иметь вид
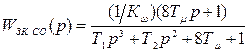 , (5.25)
, (5.25)
где 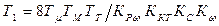 ,
, 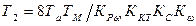 -постоянные времени.
-постоянные времени.
Системы, настроенные на симметричный оптимум, не имеют статической ошибки, но колебания возрастают, перерегулирование увеличивается до 47%. В связи с этим перед контуром скорости, как правило, включают фильтр, представляющий собой апериодическое звено.
Двухконтурная система с ПИ-регулятором скорости обладает астатизмом второго порядка [1] благодаря чему установившаяся динамическая ошибка в режимах линейного нарастания задания отсутствует. Поэтому двухкратноинтегрирующие системы применяют в тех случаях, когда необходимо иметь высокую точность отработки изменений сигналов задания. Однако в начале процесса в связи с электромагнитной инерцией происходит отставание изменения скорости от заданных значений. Возникшая при этом ошибка отрабатывается в течение времени 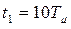 с перерегулированием по току достигающим 56% установившегося значения, что требует коррекции реакции двухконтурной системы с ПИ-регулятором скорости на изменения управляющего воздействия. Для достижения этой цели необходимо на задающий вход регулятора включить фильтр с передаточной функцией
с перерегулированием по току достигающим 56% установившегося значения, что требует коррекции реакции двухконтурной системы с ПИ-регулятором скорости на изменения управляющего воздействия. Для достижения этой цели необходимо на задающий вход регулятора включить фильтр с передаточной функцией
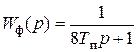 . (5.26)
. (5.26)
При введении звена (5.26) установившаяся ошибка при линейном нарастании задания получается уже не равной нулю [1], но характер переходных процессов в системе при этом соответствует настройке на технический оптимум.
Структурная схема контура скорости с ПИ-регулятором и фильтром на входе контура приведена на рис. 5.6.


Рис. 5.6. Структурная схема контура скорости с ПИ-регулятором
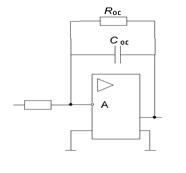
Рис. 5.7. Схема фильтра
Параметры входных цепей и цепей обратных связей ПИ-регулятора скорости рассчитывают аналогично рассмотренному ранее ПИ-регулятору тока.
Уравнению фильтра (5.26) соответствует апериодическое звено (рис. 5.7), параметры которого определяются следующими соотношениями,
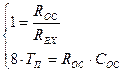 (5.27)
(5.27)
где, Сос=(0,1-2)мкФ; Rос=Rвх=(10-100)кОм.
5.4. Влияние внутренней обратной связи по ЭДС двигателя
на характер переходных процессов в СПР
При синтезе контура тока обычно влиянием обратной внутренней отрицательной связи по ЭДС двигателя пренебрегают, что приводит к значительному упрощению расчетов. Вместе с тем при определенных соотношениях параметров СПР Тм/Тя < 2 это влияние достаточно велико и должно учитываться при настройке регуляторов.
Структурная схема замкнутого контура тока с учетом обратной связи по ЭДС двигателя будет иметь вид, представленный на рис. 5.8.

Рис. 5.8. Структурная схема контура тока с учетом обратной связи по ЭДС двигателя
По данной структурной схеме (рис. 5.8) получим передаточную функцию замкнутого контура тока с учетом обратной связи по ЭДС двигателя:
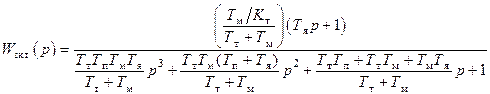 . (5.28)
. (5.28)
В статических режимах работы, учитывая что р = 0, получим коэффициент передачи контура тока с учетом влияния обратной связи по ЭДС двигателя:
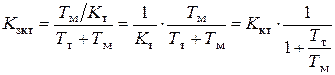 . (5.29)
. (5.29)
Установившееся значение тока в контуре уменьшается в 1/(1+Тт/Тм) раз, что приводит к недоиспользованию тока двигателя в переходных процессах. Чем меньше величина Тт = 2Тп = 2Тμ и больше величина Тм, тем меньше погрешность выходной переменной контура тока. Влияние обратной связи по ЭДС двигателя сказывается и на характере протекания переходных процессов в контуре тока повышением колебательности переменной и снижением быстродействия.
Для устранения влияния обратной связи по ЭДС двигателя могут быть использованы следующие способы:
а) некомпенсированную постоянную времени Тμ сделать как можно меньше, но в то же время обеспечивающей требуемую помехоустойчивость системы;
б) увеличить коэффициент усиления контура тока в (Тт+Тм)/Тм раз;
в) увеличить коэффициент усиления Kрω регулятора скорости;
г) в цепь обратной связи контура тока с коэффициентом передачи Kт включить дополнительное звено (рис. 5.8, 5.9) с передаточной функцией
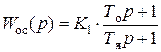 , (5.30)
, (5.30)
где 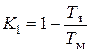 ;
; 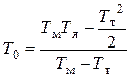 ; уменьшение обратной связи по току K1
; уменьшение обратной связи по току K1
в (1–Тт/Тм) раз приводит к увеличению установившегося тока; звено с передаточной функцией (Тор+1) /(Тяр+1) устраняет искажения формы динамического тока;


Рис. 5.9. Структурная схема цепи обратной связи контура тока
с учетом влияния ЭДС двигателя
д) применить пропорционально-интегральный регулятор тока с астатизмом второго порядка:
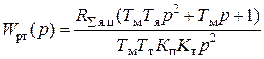 ; (5.31)
; (5.31)


Рис. 5.10. Структурная схема оптимизированного контура тока
с компенсацией влияния обратной связи по ЭДС двигателя
е) ввести в систему управления электроприводом положительной компенсирующей обратной связи по ЭДС двигателя с такой же передаточной функцией W(р) = СеФω. Компенсирующая обратная связь может быть вынесена (рис. 5.10) на вход-выход контура тока, после чего складывается с оптимизирующей отрицательной обратной связью с коэффициентом передачи Kт.
В результате получается одна отрицательная связь в контуре тока с передаточной функцией:
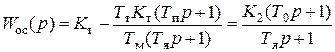 , (5.32)
, (5.32)
где 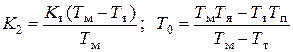 .
.
Дата добавления: 2016-12-27; просмотров: 5217;











