Случай линейных проводником с током.
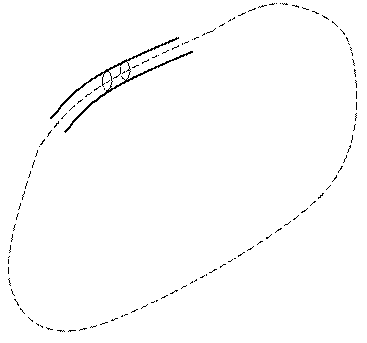
Проводники считаются линейными, когда размеры поперечного сечения проводника намного меньше его длины (рис. 8–1).
 | |||
 |

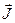
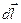
dv
r
l
Рисунок 8–1
Запишем выражение для векторного потенциала, учитывая, что направления векторов 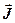 и
и 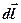 совпадают, а ток сквозь любое сечение проводника одинаков:
совпадают, а ток сквозь любое сечение проводника одинаков:
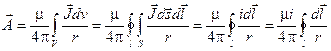 .
.
Если магнитное поле создано несколькими проводниками с токами, то следует интегрировать вдоль всех проводников с токами, тогда:
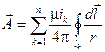
Полученные соотношения пригодны для определения векторного потенциала (его проекций) по заданному распределению плотностей тока в пространстве, как в областях вне токов ( 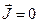 ), так и внутри проводников с токами (
), так и внутри проводников с токами ( 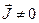 ).
).
Все полученные соотношения для определения векторного потенциала справедливы в предположении, что в магнитном отношении среда однородна m = const ≠ f(x,y,z) или кусочно - однородна. Если среда неоднородна, то нельзя выносить m за оператор ротора: 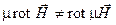 , так как
, так как 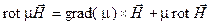 .
.
Мы ввели вспомогательный величину – векторный потенциал, вычислив который можно затем определить характеристики магнитного воля – магнитную индукцию и напряженность магнитного поля. В электрическом поле введение и отыскание скалярного электрического потенциала имеет смысл, так как проще найти скалярную функцию, а затем по ней характеристики поля. Возникает вопрос, зачем вводить и определять вспомогательную векторную функцию, если можно непосредственно рассчитать векторы индукции и напряженности магнитного поля. На первый взгляд здесь не обнаруживается никакого упрощения расчетов. Однако преимущества использования векторного потенциала наглядно проявляются при вычислении интегральных характеристик магнитного пола. Рассмотрим это на примере определения магнитного потока.
Дата добавления: 2021-04-21; просмотров: 489;











