Индуктивности массивных контуров
Определение взаимной индуктивности между двумя массивными контурами.Мы помним, что взаимная индуктивность вводится как коэффициент пропорциональности между потокосцеплением взаимоиндукции одного контура и током в другом контуре: 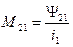 .
.
Рассмотрим два массивных контура, разбив токи в них на элементарные трубки тока (рис. 9-2).
J1 dl1
 r J2 dl2
r J2 dl2
1l22
i2
i1
Рисунок 9–2
Определим потокосцепление второго контура, созданное током в первом контуре. Вначале определим магнитный поток сквозь сечение, ограниченное контуром l2:
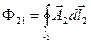 .
.
Элементарное потокосцепление с трубкой тока во втором контуре определяется отношением тока в этой трубке к полному току второго контура:
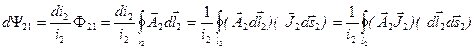 .
.
Полное потокосцепление взаимоиндукции второго контура получим, проинтегрировав полученное выражение по всем трубкам тока во втором контуре, т.е. всему объему второго контура:
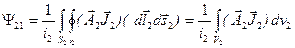 .
.
Величина векторного магнитного потенциала в точках второго контура определяется с помощью полученного ранее решения уравнения Пуассона для векторного магнитного потенциала через плотность тока в первом контуре:
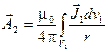 .
.
Тогда потокосцепление взаимоиндукции второго контура можем представить в виде:
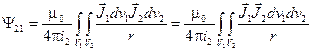 .
.
Взаимная индуктивность между вторым и первым контуром можно вычислить из соотношения:
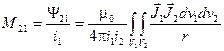 .
.
При определении взаимной индуктивности между первым и вторым контуром необходимо определить потокосцепление первого контура, задав ток во втором контуре. Проделав аналогичные вычисления, получим:
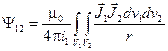 ;
; 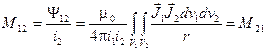 .
.
Таким образом, взаимная индуктивность между двумя контурами получается одинаковой, независимо от порядка ее вычисления, т.е. соблюдается принцип взаимности. Взаимная индуктивность не зависит от токов в контурах, так как плотности токов, стоящие в числителе, изменяются пропорционально токам контуров, стоящим в знаменателе. Взаимная индуктивность зависит от формы, размеров и взаимного расположения двух контуров и от распределения токов по сечению контуров.
Определение собственной индуктивности массивного контура.При определении собственной индуктивности применим полученную формулу для расчета взаимной индуктивности двух одинаковых, совмещенных друг с другом контуров. В этом случае токи в контурах совпадают (i1 = i2 = i), объемы контуров одинаковы (V1 = V2 = V), а взаимная индуктивность переходит в собственную индуктивность (M12 Ù L):
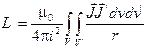 .
.
Дата добавления: 2021-04-21; просмотров: 473;











