Определение магнитного потока через векторный потенциал.

Определим магнитный поток через некоторую поверхность S, ограниченную замкнутым контуром l (рис. 8–2).

S

l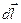

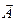
Рисунок 8–2

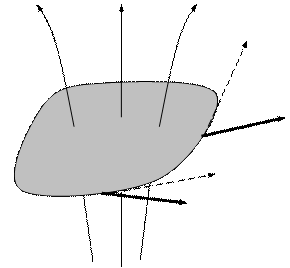
Запишем выражение магнитного потока через индукцию магнитного поля, а затем, выразив индукцию через векторный потенциал и применив теорему Стокса, получим:

.

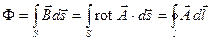Вычисление магнитного потока удобнее производить, интегрируя векторный потенциал по замкнутому контуру, так как необходимо знать векторный магнитный потенциал лишь на контуре l , ограничивающем поверхность S , и не требуется определять магнитную индукцию на всей поверхности S.

При рассмотрении граничных условий из интегралов по замкнутым контурам для векторов поля мы получали на поверхности раздела сред равенство касательных составляющих векторов. По аналогии можем записать:

A_1t = A_2t

Таким образом, на поверхностях раздела различных сред не изменяются ни нормальные, ни касательные составляющие векторного магнитного потенциала. Это означает, что при переходе из одной среды в другую векторный магнитный потенциал не изменяется ни по величине, ни по направлению.

Пример

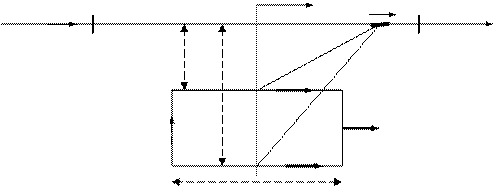
Определим магнитный поток, сцепляющийся с прямоугольной рамкой, расположенной в одной плоскости с прямолинейным проводником с током, причем две стороны рамки параллельны проводнику с током (рис.8–3).

i 0 dz

z

– L a b r₁ + L

r₂

A₁

l A_k

A₂

h

Рисунок 8–3

Выразим магнитный поток через векторный потенциал и, учитывая, что магнитное поле плоскопараллельное, и векторный потенциал имеет единственную составляющую:

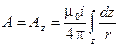, получим: .

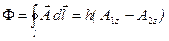Определим значения векторного магнитного потенциала (A₁ иA₂) на ближней и дальней сторонах рамки. Так как для бесконечно длинного провода векторный потенциал определить невозможно, ибо ток в проводе получается незамкнутым ( не выполняется принцип непрерывности электрического тока), то будем сразу определять разность указанных векторных потенциалов (A₁ –A₂). В этом случае влияние бесконечно удаленных концов провода с током на одну и другую сторону рамки компенсируются.

.

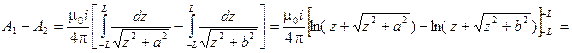
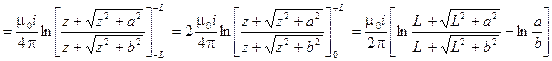При устремлении координаты L к бесконечности первый логарифм обращается и нуль, так как дробь стремится к единице, и окончательно получим:

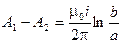и величина магнитного потока равна: .

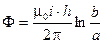Простота вычисления магнитных потоков с помощью векторного потенциала позволяет успешно использовать векторный магнитный потенциал для расчета собственных и взаимных индуктивностей.