Нечеткие числа (L-R)-Tипа

Нечеткие числа (L-R)-типа — это разновидность нечетких чисел специального вида, т.е. задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.

Функции принадлежности нечетких чисел (L-R)-типa задаются с помощью невозрастающих на множестве неотрицательных дей­ствительных чисел функций действительного переменного L(x) и R(x), удовлетворяющих свойствам:

а) L(-x) = L(x), R(-x) = R(x);

б) L(0) = R(0).

Очевидно, что к классу (L-R)-функций относятся функции, графики которых имеют вид, приведенный на рис. 1.7.

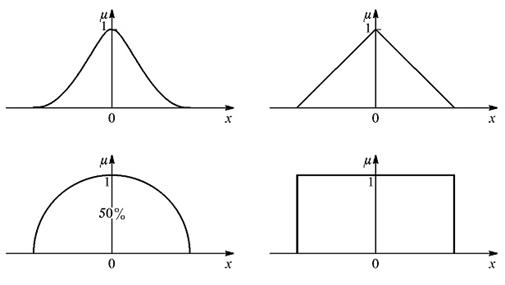
Рис. 1.7. Возможный вид (L-R)-функций

Примерами аналитического задания (L-R)-функций могут быть

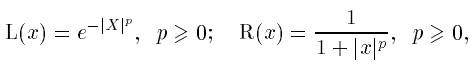
и т. д.

Пусть L(у)и R(у)— функции (L-R)-типа (конкретные). Уни­модальное нечеткое число А с модой а (т. е. μ_А(а) = 1) с помощью L(у)и R(у) задается следующим образом:

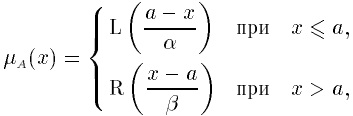
где а — мода; α > 0, β > 0 — левый и правый коэффициенты нечеткости.

Таким образом, при заданных L(у)и R(у) нечеткое число (уни­модальное) задается тройкой А = (а, α, β).

Толерантное нечеткое число задается, соответственно, четвер­кой параметров А = (a₁, а₂, α, β), где а₁ иа₂ — границы толе­рантности, т.е. в промежутке [a₁, а₂] значение функции принад­лежности равно 1.

Примеры графиков функций принадлежности нечетких чисел (L-R)-типа приведены на рис. 1.8.

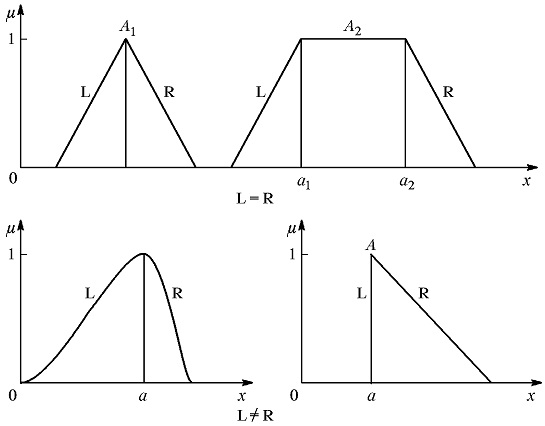
Рис. 1.8. Примеры графиков функций принадлежности нечетких чисел (L-R)-типа

Отметим, что в конкретных ситуациях функции L(у),R(у),а также параметры а, β нечетких чисел (а, α, β) и (a₁, а₂, α, β) должны подбираться таким образом, чтобы результат операции (сложения, вычитания, деления и т.д.) был точно или приблизи­тельно равен нечеткому числу с теми же L(у)и R(у),а параметры α' и β'результата не выходили за рамки ограничений на эти па­раметры для исходных нечетких чисел, особенно если результат в дальнейшем будет участвовать в операциях.

Замечание. Решение задач математического моделирова­ния сложных систем с применением аппарата нечетких множеств требует выполнения большого объема операций над разного рода лингвистическими и другими нечеткими переменными. Для удоб­ства исполнения операций, а также для ввода-вывода и хранения данных, желательно работать с функциями принадлежности стан­дартного вида.

Нечеткие множества, которыми приходится оперировать в боль­шинстве задач, являются, как правило, унимодальными и нор­мальными. Одним из возможных методов аппроксимации унимо­дальных нечетких множеств является аппроксимация с помощью функций (L-R)-типа.

Примеры (L-R)-представлений некоторых лингвистических пе­ременных приведены в табл. 1.2.

Таблица 1.2. Возможное (L-R)-представление некоторых лингвистических переменных

Нечеткие отношения

Нечеткие отношения играют фундаментальную роль в теории нечетких систем. Аппарат теории нечетких отношений используется при построении теории нечетких автоматов, при моделировании структуры сложных систем, при анализе процессов принятия решений.