Нечеткая и лингвистическая переменные

Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.

Нечеткая переменная характеризуется тройкой (α, X, А), где

α — наименование переменной;

X — универсальное множество (область определения α);

А — нечеткое множество на X, описывающее ограничения (т.е. μ_A(x))на значения нечеткой переменной α.

Лингвистической переменной (ЛП) называется набор (β, Т, X, G, М), где

β — наименование лингвистической переменной;

Т— множество ее значений (терм-множество), представляю­щих собой наименования нечетких переменных, областью опре­деления каждой из которых является множество X. Множество Т называется базовым терм-множеством лингвистической пе­ременной;

G — синтаксическая процедура, позволяющая оперировать эле­ментами терм-множества T, в частности, генерировать новые тер­мы (значения). Множество T∪G(T), где G(T) — множество сгене­рированных термов, называется расширенным терм-множеством лингвистической переменной;

М— семантическая процедура, позволяющая превратить каж­дое новое значение лингвистической переменной, образуемое про­цедурой G, в нечеткую переменную, т.е. сформировать соответ­ствующее нечеткое множество.

Замечание. Чтобы избежать большого количества символов:

1) символ β используют как для названия самой переменной, так и для всех ее значений;

2) пользуются одним и тем же символом для обозначения не­четкого множества и его названия, например терм «Молодой», явля­ющийся значением лингвистической переменной β = «возраст», одновременно есть и нечеткое множество М («Молодой»).

Присвоение нескольких значений символам предполагает, что контекст позволяет разрешить возможные неопределенности.

Пример.Пусть эксперт определяет толщину выпускаемого изделия с помощью понятий «Малая толщина», «Средняя толщина» и «Большая толщина», при этом минимальная толщина равна 10 мм, а максималь­ная – 80 мм.

Формализация такого описания может быть проведена с помощью следующей лингвистической переменной (β, Т, X, G, М), где

β — толщина изделия;

Т — {«Малая толщина», «Средняя толщина», «Большая толщина»};

X — [10, 80];

G — процедура образования новых термов с помощью связок «и», «или» и модификаторов типа «очень», «не», «слегка» и т.п. Например: «Малая или средняя толщина», «Очень малая толщина» и т.д.;

М — процедура задания на X = [10, 80] нечетких подмножеств А₁ = «Малая толщина», А₂= «Средняя толщина», A₃ = «Большая толщи­на», а также нечетких множеств для термов из G(Т)в соответствии с пра­вилами трансляции нечетких связок и модификаторов «и», «или», «не», «очень», «слегка» и других операций над нечеткими множествами вида: А⋂В,A∪В, ̅A,CONА =A², DILА = А^0,5и т. п.

Замечание. Наряду с рассмотренными выше базовыми значения­ми лингвистической переменной «Толщина» (Т = {«Малая толщина», «Средняя толщина», «Большая толщина»}) возможны значения, завися­щие от области определения X. В данном случае значения лингвистиче­ской переменной «Толщина изделия» могут быть определены как «около 20 мм», «около 50 мм», «около 70 мм», т.е. в виде нечетких чисел.

Терм-множество и расширенное терм-множество в условиях примера можно характеризовать функциями принадлежности, при­веденными на рис. 1.5 и 1.6.

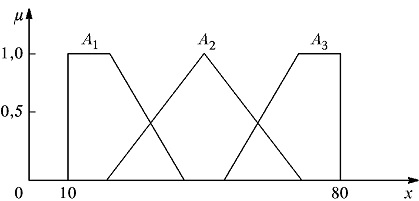
Рис. 1.5. Функции принадлежности нечетких множеств: «Малая толщина» = А₁,«Средняя толщина» = А₂, «Большая толщина» = А₃

Рис. 1.6. Функция принадлежности нечеткого множества «Малая или средняя толщина» = A₁∪ А₂

Нечеткие числа

Нечеткие числа— нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел ℝ с функцией принадлежности μ_А(х) ϵ [0, 1], где х — действительное число, т.е. х ϵ ℝ.

Нечеткое число А нормально, если тах μ_А(x) = 1; выпуклое, если для любых х ≤у ≤ z выполняется

μ_А(х)≥ μ_А(у) ˄ μ_A(z).

Множество α-уровня нечеткого числа А определяется как

Аα= {x/μ_α(x) ≥ α}.

Подмножество S_A⊂ ℝ называется носителем нечеткого числа А, если

S_A={ x/μ_A(x)> 0 }.

Нечеткое число А унимодально, если условие μ_А(х) = 1 спра­ведливо только для одной точки действительной оси.

Выпуклое нечеткое число А называется нечетким нулем, если

μ_А(0) = sup (μ_A(x)).

Нечеткое число А положительно, если ∀x ϵ S_A, х> 0 и отрицательно, если ∀х ϵ S_A, х< 0.