Треугольные нормы и конормы
Один из подходов к операторам пересечения и объединения заключается в их определении в классе треугольных норм и конорм.
Треугольной нормой(t-нормой) называется бинарная операция (двуместная действительная функция)
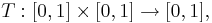
удовлетворяющая следующим условиям:
1. Ограниченность: 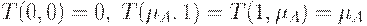 .
.
2. Монотонность: 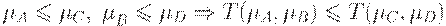 .
.
3. Коммутативность: 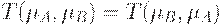 .
.
4. Ассоциативность: 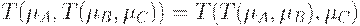 .
.
Примеры треугольных норм
min(μA,μB)
произведение μA·μB
max(0, μA+μB - 1).
Треугольной конормой (сокращенно 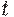 -конормой) называется двухместная действительная функция
-конормой) называется двухместная действительная функция
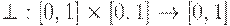 ,
,
удовлетворяющая следующим условиям:
1. Ограниченность: 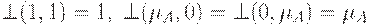 .
.
2. Монотонность: 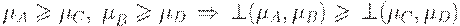 .
.
3. Коммутативность:  .
.
4. Ассоциативность:  .
.
Треугольная конорма 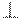 является архимедовой, если она непрерывна
является архимедовой, если она непрерывна
и для любого нечеткого множества 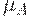 выполнено неравенство
выполнено неравенство 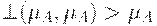 .
.
Она называется строгой, если функция  строго убывает по обоим аргументам.
строго убывает по обоим аргументам.
Примеры t-конорм
max(μA,μB)
μA+μB-μA·μB
min(1, μA+μB).
Примерами треугольных конорм являются следующие операторы:
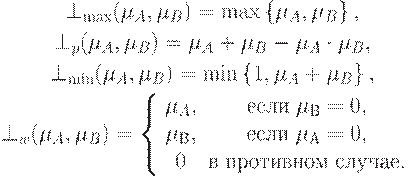
Треугольная норма T и треугольная конорма S называются дополнительными бинарными операциями, если
T(a,b) + S(1 − a,1 − b) = 1
для 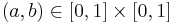 .
.
Наибольшей популярностью в теории Заде пользуются три пары дополнительных треугольных норм и конорм.
1) Пересечение и объединение по Заде:
TZ(a,b) = min{a,b}, SZ(a,b) = max{a,b}.
2) Пересечение и объединение по Лукасевичу:
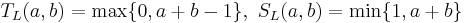 .
.
3) Вероятностное пересечение и объединение:
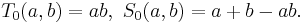
Дата добавления: 2016-12-27; просмотров: 5125;











