Расчёты в трёхфазных цепях

Пример 3.2.1

Дано: U_сети=380/220 В

Требуется: Выразить линейные и фазные напряжения сети комплексными числами.

Решение:

Изобразим систему линейных и фазных напряжений сети ( рис. 3.7.1 ) так, чтобы все шесть векторов исходили из одной точки. Масштаб векторов не указываем. Взаимная связь векторов по уравнениям (3.2.1.) и (3.2.2.) сохраняется. Поворачиваем оси комплексной плоскости так, чтобы вектор фазного напряжения U_A располагался по действительной оси. Координаты

Рис 3.7.1 расположения каждого из векторов в комплексной плоскости являются их выражениями комплексными числами:

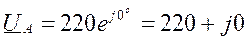
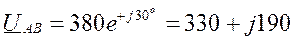
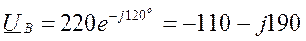
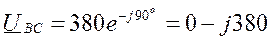
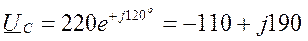
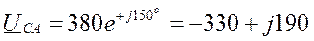
Пример 3.4.1

Дано: Схема электрических цепей, подключенных к трехфазной сети 380/220 В. R=12 Ом, X_C=5 Ом.

Требуется: Рассчитать токи, построить векторную диаграмму напряжений сети и токов.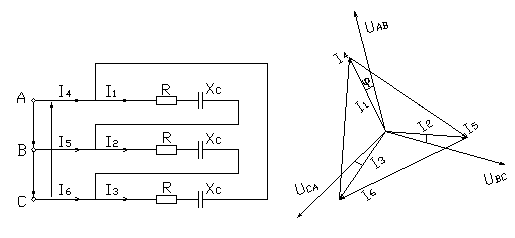

Решение:

В схеме фазы потребителя подключены к линейным напряжениям сети. Это соединение треугольником. Нагрузка симметричная. Назначаем положительные направления токов, как указано на схеме. Расчет выполняется по уравнениям (3.4.1), (3.4.2), (3.4.3).

, ,

,

,

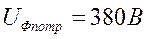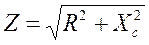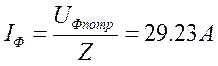
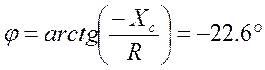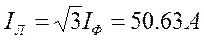
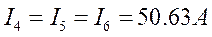
При построении векторной диаграммы указываем векторы линейных напряжений сети и токи согласно уравнениям расчета.

Пример 3.4.2

Дано: Схема электрических цепей, подключенных к трехфазной сети 380/220 В, R₁=20 Ом, X_C=40 Ом, R₃=10 Ом, X_L=10 Ом.

Требуется: Рассчитать токи, построить векторную диаграмму напряжений сети и токов.

Решение:

Фазы потребителя соединены треугольником, нагрузка несимметричная. Назначаем положительные направления токов. Для расчета токов применяем символический метод.

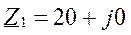
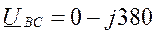
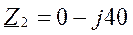
Уравнения:

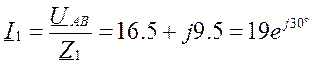
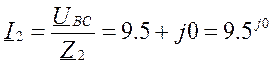
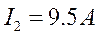
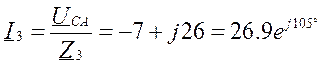
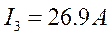
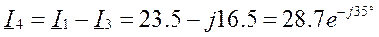
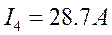
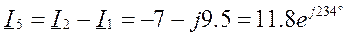
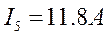
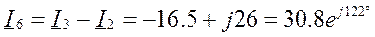
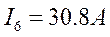
Пример 3.5.1

Дано: Четыре резистивных потребителя - нагревательные приборы, имеющие номинальные данные U_ном=220 В, P_ном,=600 Вт, подключены к трехфазной сети 380/220 В как указано на схеме.

Требуется: Определить токи, построить векторную диаграмму.

Решение:

Резисторы R₁, R₂ и параллельно соединенные R₃ и R₄ образуют соединение звездой. Нагрузка несимметричная.

Назначаем положительные направления токов, как указано на схеме.

Вычисляем величины сопротивлений:

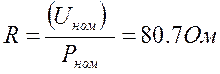
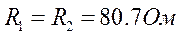
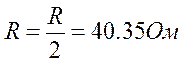
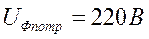
На основе уравнений (3.5.1) вычисляем токи:

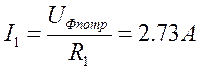
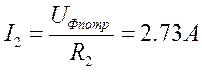
Наносим векторы токов на векторной диаграмме напряжений.

На основе уравнения (3.5.2) из векторных построений находим I₄=2.73А.

Пример 3.5.2

Дано: Схема электрических цепей, подключенных к трехфазной сети 380/220 В. R=X_L=X_C=20 Ом.

Требуется: Определить напряжения U_KM и U_KS

Решение:

Для определения U_KM выбираем вариант расчета с помощью графических построений векторов.

Векторы линейных и фазовых напряжений сети строим так, чтобы на диаграмме оказались точки с потенциалами точек схемы A, B, C, N. Взаимная связь векторов по уравнениям (3.2.1) и (3.2.2) сохраняется. Назначаем положительные направления токов как указано на схеме. Определяем токи I₁ и I₃ согласно уравнениям (3.4.1) и (3.5.1).

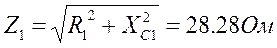
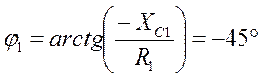
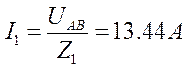
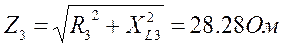
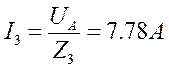
Изображаем на векторной диаграмме напряжений найденные токи как векторы.

Вычисляем напряжения: U_AK=I₁R₁=268.8 В, U_KB=I₁X_C1=268.8 В, U_AM=I₃X_L3=155.6 В, U_MN=I₃R₃=155.6 В. Изображаем на векторной диаграмме соответствующие векторы. В треугольнике KAM угол A 30⁰. По теореме косинусов вычисляем U_KM:

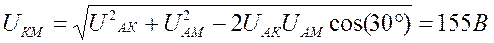
Для вычисления U_KS выбираем символический метод.

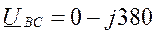
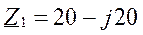
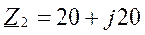
Уравнения:

,

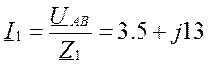
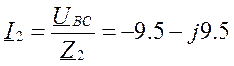
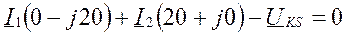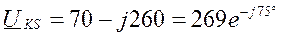
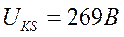
Пример 3.6.1

Дано: Схема электрических цепей, подключённых к трёхфазной сети 380/220 В.

R₁=10 Ом, R₂=20 Ом, X_L1=40 Ом, X_С2=30 Ом, X_С3=5 Ом.

Требуется: Рассчитать баланс активной и реактивной мощности.

Решение:

Фазы потребителя соединены звездой. Нагрузка несимметрич- ная. Назначаем положительные направления токов, как указано на схеме. Рассчитываем токи по уравнениям (3.5.1) символическим методом.

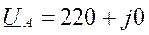
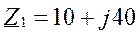
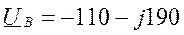
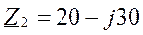
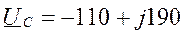
Расчёт токов:

,

,

,

,

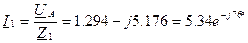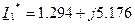
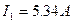
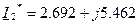
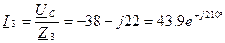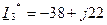
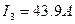
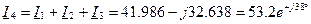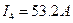
Расчёт мощности источников по уравнению (3.6.1):

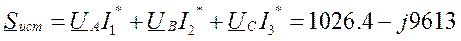
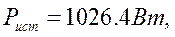
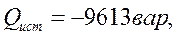
Расчёт мощности потребителей по уравнениям (3.6.2):

,

,

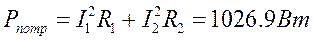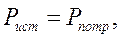
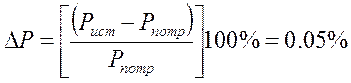
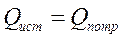
Баланс мощности сходится.

Глава 4.