Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях.

4.1. Причины возникновения периодических несинусоидальных ЭДС, токов и напряжений.

При генерировании, трансформации, распределении и потреблении электроэнергии возникают искажения формы синусоидальных ЭДС, напряжений и токов.

Несинусоидальные токи в цепях возникают при синусои­дальных ЭДС и напряжениях источников электрической энер­гии, если цепи содержат нелинейные элементы. Так, в катушке с ферромагнитным магнитопроводом, которая является нели­нейным элементом, при синусоидальном напряжении сети ток несинусоидальный. Подобное явление наблюдается в промыш­ленных городских сетях, когда в качестве осветительных при­боров используются люминесцентные лампы, имеющие нели­нейные вольт- амперные характеристики.

Нелинейные элементы широко используются в электриче­ских цепях автоматики, управления, релейной защиты и т. д. Эти нелинейные элементы (стабилизаторы напряжения, умно­жители и делители частоты, магнитные усилители и т. п.) при­водят к искажению формы кривых напряжения или тока.

Известно, что постоянный ток в энергетической электронике получают преобразованием переменного синусоидального тока с помощью выпрямителей, в которых используются нелинейные элементы — диоды. Естественно, что в таких электрических цепях возникают как несинусоидальные токи, так и несинусоидальные напряжения. На рис. 4.1.а-б приведены временные диаграммы напряжений и токов однополупериодного и двухполупериодного выпрямителей, работающих на резистивную нагрузку. В настоящее время широкое распространение получила им­пульсная техника, т. е. отрасль радиоэлектроники, в которой для решения определенных задач используют импульсные устройства. Формы импульсов на­пряжений в импульсной технике весьма разнообразны.

Основ­ное распространение получили импульсы треугольной, прямоугольной, трапецеидальной формы и др. (рис 4.2 а-в)

Появление в электрических цепях несинусоидальных напря­жений и токов может привести к весьма нежелательным по­следствиям. Несинусоидальные токи вызывают дополни­тельные потери мощности, ухудшают характеристики двигате­лей, создают большие помехи в линиях связи, каналах телемеханики и т. д. Заметим, что допустимое содержание гармоник оценивается

коэффициентом гармоник К_г. Для промышленных сетей К_г≤ 5%, т. е. в этом случае кривая напряжения на экране осциллографа визуально не отли­чается от синусоиды и это напряжение длительно допустимо на выводах любого приемника электрической энергии.

4.2 Способы представления периодических несинусоидальных величин.

Периодические несинусоидальные величины могут быть представлены временными диаграммами, тригонометрическим рядом Фурье, а также эквивалентными синусоидами. Наиболее наглядными, дающими полное представление о несинусоидаль­ной величине являются временные диаграммы, т. е. графики за­висимости мгновенных значений от времени (рис. 4.2-4.3)

Несинусоидальные ЭДС, токи и напряжения, с которыми приходится встречаться в электротехнике и промышленной электронике, являются периодическими функциями, удовлетво­ряющими условиям Дирихле и, следовательно, могут быть представлены тригонометрическим рядом Фурье:

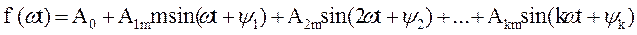Тригонометрический ряд может быть представлен как в ви­де суммы синусов (синусный ряд), так и суммы косинусов (ко­синусный ряд) гармонических составляющих.

В зависимости от характера реальной кривой f(ωt) тригоно­метрический ряд может не содержать постоянной состав­ляющей, четных или нечетных высших гармоник, а также на­чальных фаз. Например, тригонометрические ряды Фурье некоторых несинусоидальных напряжений имеют вид:

напряжение на нагрузке при однополупериодном выпрямле­нии (см. рис.4.1,а)

напряжение на нагрузке при двухполупериодном выпрямле­нии (см.рис. 4.1,б)

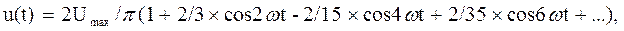
напряжение треугольной формы (см. рис 4.2,а)

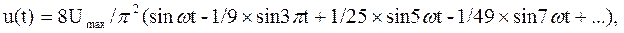
напряжение прямоугольной формы (см. рис. 4.2,б)

В практических расчетах цепей с несинусоидальными ЭДС, токами и напряжениями их мгновенные значения приближенно отображают конечным рядом Фурье (3—7 членов ряда). Число членов ряда определяется необходимой точностью расчета.

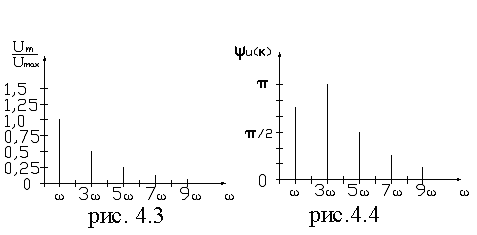
Характеристика несинусоидальных величин, представленных рядом Фурье, может быть осуществлена графически с по­мощью диаграмм амплитудно-частотного (рис. 4.3), фазо-частотного (рис. 4.2) спектров.

Данные диаграммы характеризуют форму несинусоидальных кривых, причем первая диаграмма показывает спектральный состав по амплитудам, т. е. представ­ляет зависимость амплитуд гармоник в относительных еди­ницах от частоты, вторая диаграмма выражает зависимость начальных фаз гармоник от частоты.

Периодические несинусоидальные ЭДС, напряжения и токи могут быть представлены так же эквивалентными синусоидами (см. параграф 4.5.)

4.3 Основные соотношения для несинусоидальных величин.