Соединение треугольником.

При соединении фаз потребителя треугольником каждая из фаз подключается на Рис № 3.4.1

линейное напряжение. Такое соединение представлено на рис 3.4.1а. В схеме фазы потребители имеют активно-индуктивный характер. Нагрузка симметричная.

Для расчета токов параметры сопротивления фаз должны быть заданы. Назначаются положительные направления токов. Линейных токов от источника сети к потребителю, фазных токов - по направлению приложенных к фазам потребителя напряжений сети.

Соотношения для расчета фазных токов соединения треугольником:

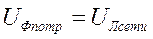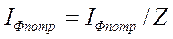, (3.4.1)

где для каждой из фаз:

,

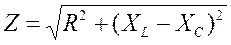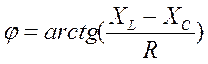
Линейные токи определяются на основе уравнений по первому закону Кирхгофа в векторной форме:

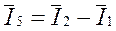(3.4.2)

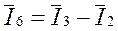
Нейтральный провод, предоставляющий потребителю фазные напряжения сети, не используется.

При симметричной нагрузке Z и φ для каждой из фаз потребителя одинаковы. Поэтому фазовые токи потребителя равны и имеют взаимный фазовый угол 120º. На векторной диаграмме рис 3.4.1б представлены векторы линейных напряжений, векторы фазных токов, соответствующие активно-индуктивному характеру нагрузки и векторы линейных токов по уравнениям (3.4.2). Линейные токи при симметричной нагрузке также равны и имеют взаимный фазовый угол 120º. Линейный ток равен удвоенной проекции вектора фазного тока под углом 30º.

При симметричной нагрузке:

(3.4.3)

Расчет токов для соединения треугольником при симметричной нагрузке приведен в примере 3.4.1.

При несимметричной нагрузке аналитический расчёт токов следует выполнять символическим методом. Справедливы общие правила составления уравнений. Необходимо рассчитать шесть токов. Схема имеет четыре узла: три в соединении треугольником и один в источнике. Независимые уравнения по первому закону Кирхгофа соответствуют уравнениям (3.4.2.). Уравнения, составленные по второму закону Кирхгофа, включающие линейные напряжения и разрешённые относительно тока - это три уравнения, соответствующие уравнениям (3.4.1). Расчёт приведён в примере 3.4.2.