Модель с логарифмическим уравнением, называемым «эмиссионным».
Логарифмические уравнения решаются очень не просто - их приходится решать на ЭВМ методом подбора. В основном все графические построения выполнены на основе подпрограммы, способной подбирать решение, поэтому вместе с графиками будут приводиться листинги подпрограмм, обеспечивающих построение этих графиков.
История проблемы.
В 1.4.2.1. рассматривается математическая модель двухполюсника, состоящего из идеального диода и резистора. Решение для этой модели описывается логарифмическим уравнением, которое решается при помощи подпрограммы подбора решения – Midi.
В 1.4.2.4. выясняется, что тем же уравнением описывается решение для системы с ООС для экспоненциальной функции, а значит, эта задача решается той же подпрограммой Midi и имеет аналогичные графики.
Реальные кремниевые полупроводниковые диоды при моделировании имеют в качестве модели такое же логарифмическое уравнение. Это значит, что одна ООС внутри процесса для ВАХ полупроводникового диода уже существует. Но если мы начинаем изменять температуру Т, то логарифмическое уравнение принимает более сложный – двухмерный вид. Такое уравнение и называется «эмиссионным». Кроме того, существуют определённые условия, когда эмиссионное уравнение является внешней функцией для моделирования двухмерного процессового перехода для двух процессов, ограничивающих друг друга ( для двух комплиментарных процессов ).
Попробуем изложить математику логарифмических уравнений. В общем случае эмиссионное уравнение записывается так:
y рез = exp( -K1* ( (x-x0)*(z-z0) – K2*z))
Для нашей физики процесса х – это напряжение, z – температура, K1 и K2 - коэффициенты, регулирующие кривизну участка перехода между процессами.
х и z – аргументы сигналов прямой связи ( аргументы прямой связи ),
x0 и z0 – аргументы сигналов обратной связи ( аргументы обратной связи ).
Общий вид эмиссионного уравнения:
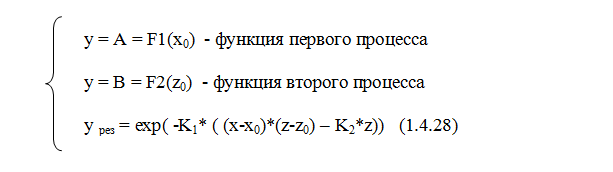
Логарифмическое уравнение (1.4.28) является внешней функцией по отношению к функциям A и B.
В результате эмиссионное уравнение выглядит так:
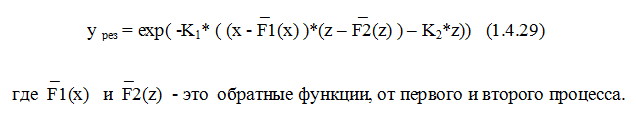
Дата добавления: 2021-04-21; просмотров: 688;











