Математическая модель с логарифмическим «эмиссионным» уравнением для полупроводникового диода.

ВАХ полупроводникового диода в условиях изменения температуры ещё нуждаются в изучении. Кремниевые диоды (как их называют) показывают некоторое совпадение своих ВАХ с эмиссионным уравнением, которая выглядит следующим образом:

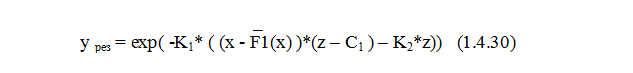
где С₁ – некоторая константа.

Возможно, процесс B имеет очень малое изменение, поэтому экспериментально вместо него обнаруживается константа С₁ - обычно константа С₁ в эмиссионном уравнении обозначается как T_F (температура «фокуса»), для кремниевых диодов она равна приблизительно 600 Кельвин. В таких условиях, когда отсутствует ООС по отношению к z, логарифмическое уравнение выражает собой только одну ООС по отношению к переменной x.

Из раздела 1.4.4.2. (общий случай обратной связи) мы делаем вывод, что экспоненциальная функция является внешней при описании перехода от процесса к процессу. Уравнение (1.4.30) имеет две переменные, но только одну ООС, поэтому в (1.4.30) процессы относительно x и z не являются комплиментарными. Преобразуем формулу (1.4.30) следующим образом:

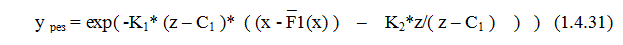
Формула (1.4.31) отображает влияние параметра z на ООС, в которую включен параметр x.

Логарифмические уравнения зависят от масштабов функций-процессов, и тем более, если в уравнении присутствуют коэффициенты-регуляторы кривизны переходов между процессами. Потому рассмотрим практический пример – эмпирическое уравнение для ВАХ кремниевого полупроводникового диода КД 213А. У неё есть ряд особенностей, отличающих её в физике от эффекта Пельтье. Так, например, ВАХ прямого тока КД 213А не пересекает ось ОХ и не пересекает ось ОY, а проходит через точку (0,0) согласно закону Ома - это так называемый «полупроводниковый эффект Пельтье», в котором отсутствует эффект Зеебека (термо-ЭДС ) и отсутствует холодильный эффект Пельтье.

Математическая модель , использующая эмиссионное уравнение, имеет свой диапазон применимости – так, она не соответствует физике процессов в кремниевых диодах при значениях аргумента менее 0,1 В. При значениях аргумента более 0,1 В модель в точности совпадает с экспериментальными данными. Кроме того, её можно сравнить с ВАХ термопары. По температуре реальные физические процессы ограничены температурой сверху - для кремния не более 100 градусов Цельсия. В математической модели можно наблюдать любые температуры, если это представляет математический интерес.

Общий вид эмиссионного уравнения для кремниевого полупроводникового диода:

Общий вид эмиссионного уравнения для кремниевого полупроводникового диода КД 213А:

Ia = exp( -K_T*( (Ua - U_B)* ( Т - T_F ) - T* U_D ) ) (1.4.32)

где:

K_T = 0,0956

T_F =605,2 Kельвин,

U_B = 0,885 + Ia* 0.25 = U_V + Ia* R_D – обратная функция от функции процесса,

U_D = 0.276 Вольт,

T < T_F,

U_V = 0.885 Вольт,

R_D = 0.25 Ом.

Найдём функцию процесса:

Ia = (1/R_D) *( Ua - Uv ) = 4*(Ua – 0,885) = 4*Ua – 3,54

Учитывая уравнение (1.4.27), можно рассчитать процесс, зависимый от температуры. Это поможет найти процесс как асимптоту ( или похожее на неё ).

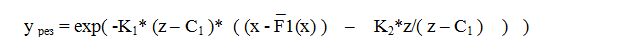
Ia = exp( -K_T* ( Т - T_F )* ( Ua - U_B - T* U_D/( Т - T_F ) ) ) (1.4.33).

Тогда:

U_B + U_D*T/( Т - T_T ) = 0,885 + Ia* 0.25 + 0,276* T/( Т - T_T )

Отсюда:

Ua = U_V + Ia* R_D + U_D* T/( Т - T_F )

Ia = ( 1/R_D )*( Ua – U_V –U_D* T/( Т - T_F ) ( 1.4.34)

Ia = 4* (Ua -0,885 – 0,276* T/( Т - T_F ) ) = 4*Ua – 3,54 - 1,104* T/( Т - T_F )

На рис. 1.4.30. построен график функции для температуры 20 градусов Цельсия синими точками. Тут же построен зелёными точками график функции

F3(Ua) = Ia = 4*Ua – 3,54 - 1,104* T/( Т - T_F )

Функция F3(Ua) является расширенной функцией процесса A, она состоит из трёх слагаемых. Ток ООС состоит из 3 –х составляющих:

+ 4*Ua – это ток ООС на проводимости 4 Сименс,

– 3,54 Ампер – постоянная составляющая,

- 1,104* T/( Т - T_F ) Ампер – температурная составляющая.

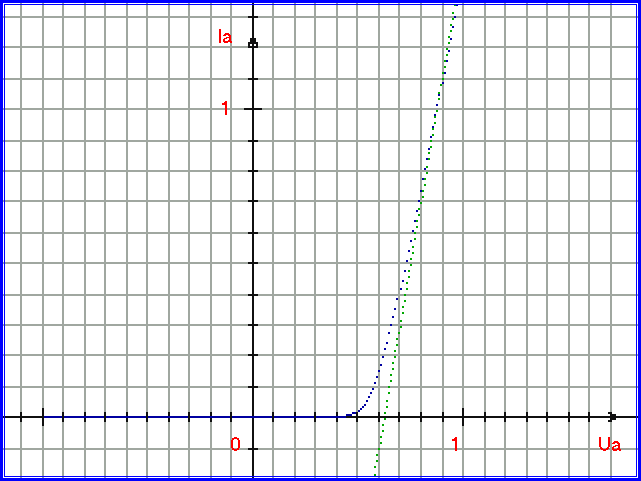
Рис. 1.4.30. График, иллюстрирующий одномерный процессовый переход для процесса A =F3(Ua) = Ia = ( 1/R_D )*( Ua – U_V –U_D* T/( Т - T_F ) (показан зелёными точками) и процесса B = Ia = 0, синими точками построена функция Ia_рез = exp( -K_T*( (Ua - U_B)* ( Т - T_F ) - T* U_D ) ). Ось аргумента - в Вольтах, ось функции - в Амперах.

Подпрограмма, вычисляющая функцию Ia_рез :

На графике 1.4.30. видно, что процесс А не является асимптотой, хотя и близок к асимптоте. Возможно, это свойство численного решения логарифмического уравнения (во всяком случае, это надо доказать). Верность вычисления решения логарифмического уравнения зависит и от алгоритма вычисления, который необходимо проверять, чтобы не было ошибок вычисления. В дальнейшем можно рассмотреть несколько примеров моделирования комплиментарных процессов при помощи эмиссионного уравнения.