Уравнение относительного движения точки
Приведенная выше информация относилась к задачам о движении точки в инерциальных системах отсчета, т.е. таких системах отсчета, где выполняется первый закон динамики (закон инерции).
Это означает, что в инерциальных системах отсчета при равенстве нулю правой части основного закона динамики (11.1) ускорение точки равно нулю. В противном случае, система отсчета является неинерциальной. В таких системах использовать основной закон или дифференциальные уравнения движения точки (12.2) не представляется возможным. Выведем уравнение, описывающее движение материальной точки в неинерциальной системе.
Пусть точка совершает сложное движение, представляющее собой сумму относительного и переносного движений. Тогда, ускорение точки относительно неподвижной системы от-
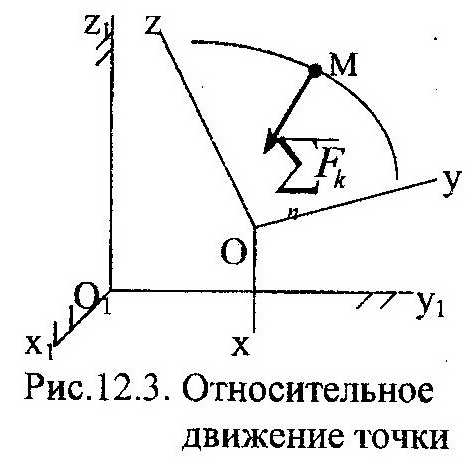
| счета, x1O1y1z1 (рис. 12.3), аа – абсолютное ускорение, равно:
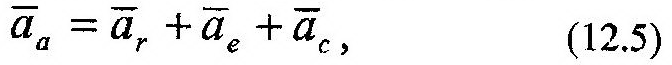
| |
| где | 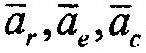
| – относительное, переносное и корио- |
лисово ускорения соответственно.
Подставим (12.5) в (11.1), получим:
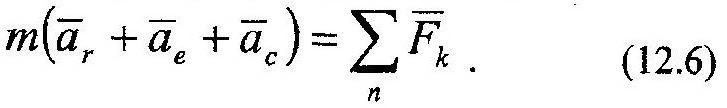 Решим это уравнение относительно ar – параметра, со-
Решим это уравнение относительно ar – параметра, со-
|
ответствующего движению точки относительно подвижной системы отсчета:
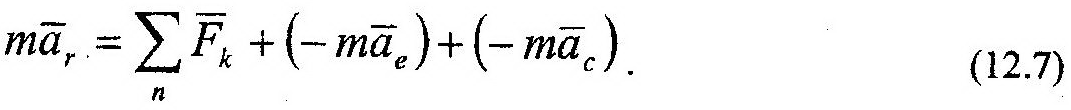
Второе и третье слагаемые в (12.7) имеют размерность силы и называются переносной,
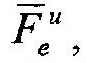
| и кориолисовой, | 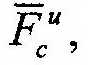
| силами инерции: |
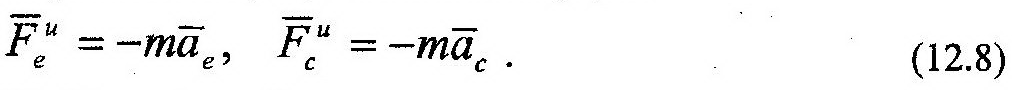
Согласно (12.8) направление действия сил инерции противоположно направлениям соответствующих векторов ускорений, а их модули равны:

В общем случае уравнение динамики относительного движения точки имеет следу-ющий вид:
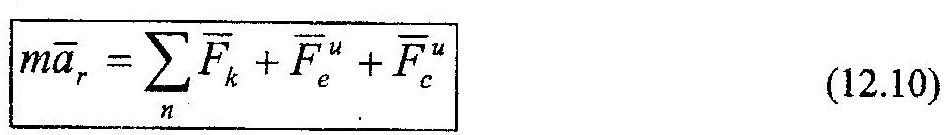
Спроектировав (12.10) на координатные оси, получим:
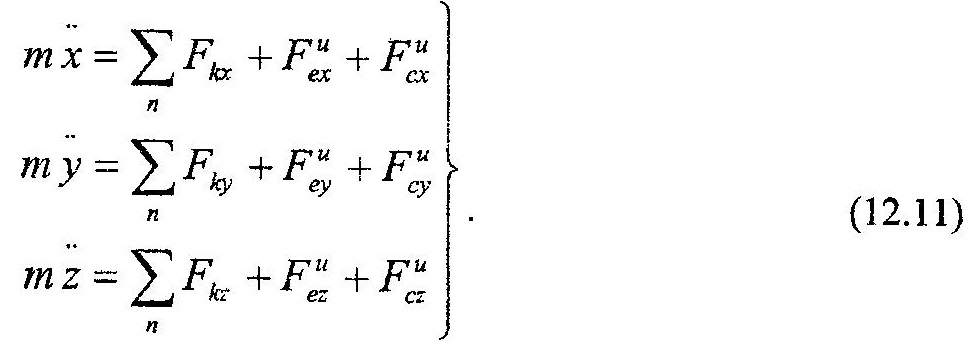
Анализируя (12.10) и (12.11), можно сделать следующие выводы, что при рассмотрении движения материальной точки относительно подвижной системы отсчета:
| - необходимо к ней, кроме фактически приложенных сил, | 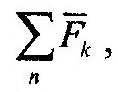
| приложить дополни- | ||||
| тельную переносную, | 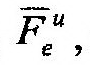
| и кориолисову, | 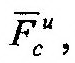
| силы инерции; | ||
- закон инерции (1-й закон динамики), в общем случае, выполняться не будет. Только в случае равномерного прямолинейного поступательного движения подвижной системы отсчета второе и третье слагаемые в правых частях (12.10) и (12.11) обращаются в нуль, и тогда закон инерции будет выполняться.
Дата добавления: 2016-12-16; просмотров: 1870;











