Дифференциальные уравнения движения системы

<19 20 212223 24 25 >

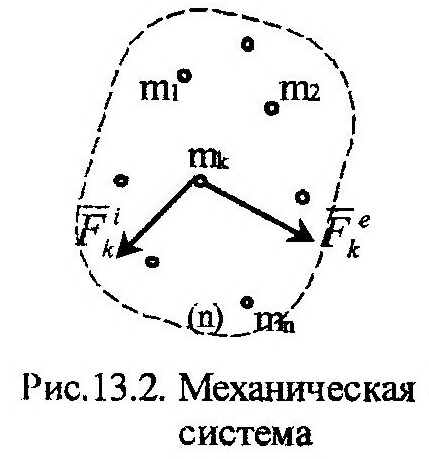
	Рассмотрим механическую систему, состоящую из n материальных точек (рис. 13.2). Для описания движения всей системы необходимо найти уравнения движения каждой точки. Пусть на произвольную k-ю точку систе-мы действуют силы, которые могут быть поделены на внешние и внутренние, на основе приведенной выше классификации. Поскольку все силы приложены к точке, постольку они образуют две системы сходящихся сил: внешних и внутренних. Найдем равнодействующие этих
систем:		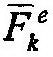и		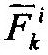(рис. 13.2).

Для написания уравнения k-й точки используем выражение основного закона динамики (11.1). При этом его правую часть представим как сумму двух сил, получим:

Аналогичное выражение можно получить для всех точек механической системы. Объединяя эти выражения, получим систему (13.6) дифференциальных уравнений дви-

жжения механической системы. Проведем ее анализ. Описание движения механической системы таким путем связано с получением уравнений для каждой точки. С одной стороны, этот путь позволяет наиболее точно решить данную задачу. Однако, на этом пути неизбежно возникают технические проблемы, связанные с нахождением всех внешних и внутренних сил, действующих на все точки систе-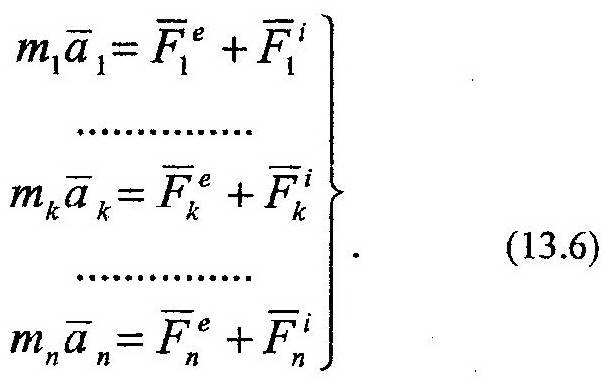

мы. Кроме того, решение системы (13.6) с большим числом уравнений неизбежно связано с неприемлемой затратой машинного времени, что также не всегда реализуемо в инженерной практике. В то же время, решение инженерных задач зачастую не требует такой детализации в описании движения механической системы, которую подразумевает система дифференциальных уравнений (13.6). Обычно требуется установить изменение некоторых общих кинематических характеристик механической системы. В этом случае наиболее рациональным путем решения задачи является использование так называемых общих теорем динамики, к рассмотрению которых мы и переходим.

<19 20 212223 24 25 >

Дата добавления: 2016-12-16; просмотров: 1277;