Модель экономического роста Рамсея (Рамсея – Касса – Купманса)

Модель Ф. Рамсея – Д. Касса – Т. Купманса или модель Рамсея – модель эндогенного экономического роста, в которой «траектория» потребления и сбережений определяются на основе решения задачи оптимизации домашних хозяйств и фирм в условиях совершенной конкуренции.

Ее составными частями стали:

1) условие оптимальности и межвременная функция полезности домохозяйств Ф. Рамсея (1928);

2) метод оптимального потребления в неоклассической модели роста на основе эндогенной ставки сбережения Д. Касса (1965) и Т. Купмпанса (1963).

В модели используется репрезентативное домашнее хозяйство с динамикой его потребительского и сберегательного поведения. Предполагается закрытая экономика с реальными переменными (в единицах товаров и услуг) в условиях совершенной конкуренции. Условно предполагается, что решения этого домохозяйства эквивалентны решениям бесконечно живущего индивида, который учитывает текущее и будущее благосостояние и ресурсы. Задача потребительского выбора или функция полезности этого индивида, представляющего все население, имеет вид:

,

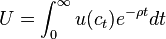где 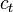– потребление на душу населения в момент времени .

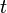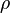– положительный коэффициент дисконтирования, отражающий межвременные предпочтения индивида.

Функция полезности 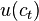является сепарабельной, то есть зависит только от потребления в этот момент. Кроме этого, предполагается что предельная полезность – производная u'(c) – является положительной и убывающей функцией и при стремлении потребления к нулю, предельная полезность стремится к бесконечности, а при стремлении потребления к бесконечности предельная полезность стремится к нулю.

Доходы «индивида» складываются из заработной платы 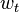и доходов 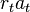от активов 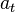, принадлежащих ему и имеющих доходность 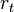(активы могут быть также и отрицательными, что отражает ситуацию чистого долга, причем ставка по заемным средствам предполагается одинаковой с доходностью положительных активов). При этом доходы тратятся либо на потребление, либо на увеличение активов (сбережения). Таким образом, увеличение активов в единицу времени равно 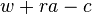. Необходимо также учесть, что население растет темпом 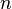, поэтому активы на одного человека сокращаются с этим же темпом, то есть скорость изменения активов в каждый момент времени уменьшаются на 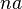. Таким образом, окончательно бюджетное ограничение индивида имеет вид

.

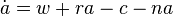Задача оптимизации поведения потребителя заключается в максимизации 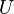при данном ограничении. Cтроится функция Гамильтона:

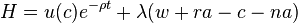
и условия максимума

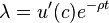и .

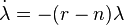Отсюда выводится уравнение динамики потребления:

,

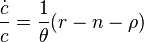где 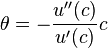– эластичность предельной полезности по потреблению.

Эта эластичность является положительной в силу положительности предельной полезности и отрицательности второй производной полезности (убывающая предельная полезность).

Для существования стационарного состояния необходимо, чтобы 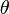асимптотически стремилась к постоянной величине, поэтому в качестве функции полезности 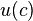используют функцию следующего вида:

,

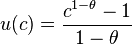где 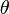– постоянная эластичность предельной полезности по потреблению.

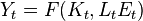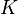Помимо задачи потребителя в модели также решается и задача фирмы. Рассматривается репрезентативная фирма, производственная функция которой описывает совокупное предложение. Производственная функция является неоклассической и аналогичной производственной функции в модели Солоу: , где – капитал, 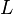– труд, 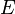– эффективность труда. Предполагается, что эффективность труда растет с постоянным темпом .

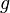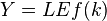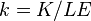В силу однородности функции можно записать , где – капиталовооруженность труда с постоянной эффективностью. Тогда

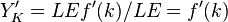– предельная производительность труда,

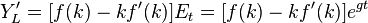– предельная производительность труда, где в целях упрощения, предполагается, что эффективность труда в нулевой момент времени равна единице, поэтому динамика эффективности труда описывается как .

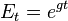В условиях совершенной конкуренции предельные производительности по факторам производства равны ценам этих факторов. Цена трудовых ресурсов равна заработной плате 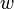, а цена капитала равна 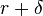, где 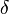– темп износа капитала. Тогда

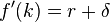
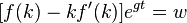
Поскольку рассматривается закрытая экономика, то капитал принадлежит резидентам и удельный капитал на одного работника (K/L) равен активам .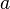

По аналогии с моделью Солоу можно записать уравнение динамики капиталовооруженности труда с постоянной эффективностью:

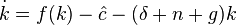
где 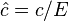– потребление на единицу труда с постоянной эффективностью.

Учитывая, что 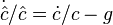, исходя из решения задачи потребителя можно записать следующее уравнение

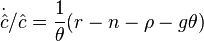
или с учетом равенства 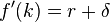в задаче фирмы:

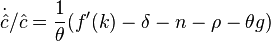
Данное дифференциальное уравнение вместе с дифференциальным уравнением для капиталовооруженности 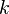и определяют экономическую динамику в рамках данной модели.

В модели Солоу устанавливалось «золотое правило» сбережений, максимизирующее потребление. В модели Рамсея это правило модифицируется и имеет вид:

,

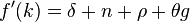что соответствует постоянному потреблению на единицу труда с постоянной эффективностью (или рост потребления на одного человека с темпом ).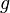

Модель объясняет основные макроэкономические закономерности, однако не объясняет причин мирового экономического роста. Общий долгосрочный рост в этой модели обеспечивает параметр эффективности труда, который не объясняется в модели, а задаётся экзогенно.

В модели Рамсея динамическая неэффективность отсутствует, поскольку выбор нормы сбережения является результатом оптимального решения экономических агентов.