Модели экономического роста Лукаса и Ромера

Модель Р. Лукаса представляет два аспекта объяснения человеческого капитала. С одной стороны, рассматривается общий уровень умений (профессионализма) (general skill level), воплощаемый в производительности лиц, занятых в производстве. Этот уровень (h) колеблется в интервале 0 < h < 1. Производственный ресурс (N) – это не просто число людей, занятых в производстве, а люди с учетом присущего им уровня умений: N = N(h). С другой стороны, речь идет о запасе человеческого капитала. Модель учитывает то, что в каждом обществе формируется определенный средний запас человеческого капитала (h_а), на его накопление направлена часть времени кроме того, которое посвящено собственно производственной деятельности. Накопление человеческого капитала рассматривается как проявление социальной активности.

С первым аспектом трактовки человеческого капитала – уровнем профессионализма занятых – связывается его внутренний эффект. Он воплощается в большей производительности и большем доходе собственника этого ресурса. Со вторым аспектом – формированием определенного, среднего для общества, запаса человеческого капитала связывается внешний эффект – выгода для всех субъектов экономики. Предусматривается, что факт существования общей выгоды от запаса человеческого капитала не принимается во внимание отдельными субъектами при распределении времени на занятость собственно производительной деятельностью (u) и накопление человеческого капитала (1 – u).

Указанные положения о человеческом капитале воплощаются в динамической производственной функции вида

Y(t) = N(t)∙c(t) + K(t) = A∙K(t)^β∙[u(t)∙h(t)∙N(t)]^1-β∙h_a(t)^y, (2.48)

где N(t)∙c(t) – сумма расходов на потребление домохозяйств;

K(t) – сумма расходов на прирост капитала;

А – постоянная величина, отражающая уровень технологий;

K(t) – запас физического капитала;

[u(t)∙h(t)∙N(t)] – показатель эффективной рабочей силы;

h_a(t)^r – внешний эффект от запаса человеческого капитала для общества;

t – период времени.

Производственная функция (2.48) отражает оба аспекта человеческого капитала. То, что он есть проявление определенного уровня умений (профессионализма), представлено корректировкой количества занятых N(t) на уровень умений h(t) и на долю времени, уделенного собственно производственной деятельности u(t). То, что запас человеческого капитала имеет позитивный внешний эффект, который увеличивает общий выпуск, отражено множителем h_α(t)^y.

Производственная функция (2.48) предусматривает возрастающую отдачу ресурсов, поскольку β + (1 – β) + γ > 1. Факт роста отдачи связан именно с появлением позитивных внешних эффектов от запаса человеческого капитала.

Модель П. Ромера основана на разграничении структурных элементов человеческого капитала. Это структурирование дает возможность избавиться от двузначности. Основной смысл структурирования – отражение различного влияния составляющих человеческого капитала на продукт (выпуск). Такими составляющими являются:

L – физические способности лиц, занятых в производстве;

Е – образование по результатам обучения в начальной и средней школе;

Z – совокупный опыт, приобретенный в процессе работы;

S – научные знания (опыт), полученные после средней школы.

Есть принципиальное отличие между L, Е, Z, с одной стороны, и S – с другой. Здесь допускается, что научные знания S вносят непосредственный вклад в создание предметов потребления. Поэтому производственная функция в части создания предметов потребления имеет следующий вид:

C = C(L^C,E^C,Z^C,X^C), (2.49)

где С – производство предметов потребления;

X^С – промежуточный продукт, используемый в производстве конечной продукции.

Хотя в уравнении (2.49) отсутствуют переменные, отражающие научные знания (S), а также физический капитал (К), они присутствуют там опосредованно – через переменную X. Объяснение механизма этого опосредованного влияния побуждает к дальнейшей детализации понятия «научные знания»: в модели различаются прикладная и фундаментальная наука. Именно прикладная наука обеспечивает развитие сектора исследований и разработок (R&D) и материализуется в продуктах. В частности, под влиянием прикладной науки происходит увеличение перечня товаров промежуточного производства (X). С учетом именно такого влияния прикладных знаний и происходит модификация производственной функции. В привычном (как функция Кобба – Дугласа) виде она такова:

G(L,E,Z,X) = L^α∙E^β∙Z^γ∙ 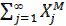. (2.50)

Причем предусматривается тождество производственных функций для потребительских (С) и капитальных (промежуточного потребления X_j) товаров. Следовательно, выполняется условие: G(L,E,Z,X) = X_j(L, E,Z,X) = C(L, E, Z, X).

Последнее иллюстрирует влиятельность прикладных научных знаний для всей экономики.

В этой модели речь идет о неизменной отдаче ресурсов, то есть о возможности устойчивого экономического роста, поскольку α + β + γ + μ = 1.

Особого внимания заслуживает такое уточнение П. Ромера о роли образования: экономический прогресс обеспечивается не приростом показателя образования (Е), а его достигнутым уровнем. Этот вывод сделан на основе регрессионного анализа. Выяснено, что существует тесная связь между показателем уровня грамотности населения и инвестициями. А уже инвестиции (и накопление физического капитала) существенно воздействуют на темп экономического роста. Эту логическую цепочку можно представить следующим образом: Е → I → К → у.