Матрица парных сравнений, определяющая зависимость судов по каждому критерию
| А1 (К1) | А1 | А2 | А3 | Приоритеты | А2 (К1) | А1 | А2 | А3 | Приоритеты | |
| А1 | 0,54 | А1 | 0,65 | |||||||
| А2 | 1/2 | 0,36 | А2 | 1/5 | 1/2 | 0,12 | ||||
| А3 | 1/4 | 1/5 | 0,1 | А3 | 1/3 | 0,23 | ||||
| ОС=0,081 | ОС=0,003 | |||||||||
| А3 (К1) | А1 | А2 | А3 | Приоритеты | ||||||
| А1 | 0,64 | |||||||||
| А2 | 1/3 | 0,29 | ||||||||
| А3 | 1/7 | 1/6 | 0,07 | |||||||
| ОС=0,086 | ||||||||||
| А1 (К2) | А1 | А2 | А3 | Приоритеты | А2 (К2) | А1 | А2 | А3 | Приоритеты | |
| А1 | 0,53 | А1 | 0,68 | |||||||
| А2 | 1/2 | 0,33 | А2 | 1/4 | 0,2 | |||||
| А3 | 1/3 | 1/3 | 0,14 | А3 | 1/5 | 1/2 | 0,12 | |||
| ОС=0,046 | ОС=0,02 | |||||||||
| А3 (К2) | А1 | А2 | А3 | Приоритеты | ||||||
| А1 | 0,69 | |||||||||
| А2 | 1/4 | 0,22 | ||||||||
| А3 | 1/6 | 1/3 | 0,1 | |||||||
| ОС=0,046 | ||||||||||
| А1 (К3) | А1 | А2 | А3 | Приоритеты | А2 (К3) | А1 | А2 | А3 | Приоритеты | |
| А1 | 0,64 | А1 | 1/7 | 0,14 | ||||||
| А2 | 1/3 | 0,27 | А2 | 1/2 | 1/6 | 0,1 | ||||
| А3 | 1/6 | 1/4 | 0,09 | А3 | 0,76 | |||||
| ОС=0,046 | ОС=0,069 | |||||||||
| А3 (К3) | А1 | А2 | А3 | Приоритеты | ||||||
| А1 | 0,7 | |||||||||
| А2 | 1/4 | 0,24 | ||||||||
| А3 | 1/9 | 1/6 | 0,06 | |||||||
| ОС=0,093 |
Для получения окончательных приоритетов взаимозависимости альтернатив, каждый столбец, полученных в табл. 2.17 умножается на каждый столбец приоритетов, полученных в табл. 2.12. Таким образом, имеем:
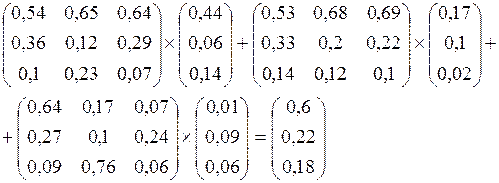
Для сравнения приоритетов при независимости и зависимости альтернатив сформируем таблицу 2.18.
Таблица 2.18
| Альтернативы | При независимости | При зависимости |
| Балкер | 0,62 | 0,6 |
| Рудовоз | 0,16 | 0,22 |
| Углевоз | 0,22 | 0,18 |
Полученные результаты говорят о том, что балкер остается лучшей альтернативой.
Задача определения приоритетов альтернатив в условиях их зависимости от критериев. Такая задача может быть представлена простой сетью с циклом, характеризующим двунаправленную связь между критериями и альтернативами (рис.2.27). Парные сравнения в такой сети выполняются в два этапа [34]. На первом этапе альтернативы (типы судов) сравниваются по каждому из критериев.
Затем выполняются парные сравнения критериев для каждого типа судов. При этом задавались вопросы: какое из двух судов в большей степени удовлетворяет критерию? Какой из двух критериев, является более характерным для данного типа судна? Данные сравнения представлены в таблицах 2.19 и 2.20.
Таблица 2.19
Парные сравнения альтернатив относительно критериев
| Фактор (К1) | А1 | А2 | А3 | Приоритеты | Фактор (К2) | А1 | А2 | А3 | Приоритеты | |
| А1 | 0,65 | А1 | 0,63 | |||||||
| А2 | 1/3 | 0,23 | А2 | 1/4 | 0,22 | |||||
| А3 | 1/5 | 1/2 | 0,12 | А3 | 1/3 | 1/2 | 0,15 | |||
| ОС=0,0032 | ОС=0,093 | |||||||||
| Фактор (К3) | А1 | А2 | А3 | Приоритеты | ||||||
| А1 | 0,63 | |||||||||
| А2 | 1/5 | 1/4 | 0,1 | |||||||
| А3 | 1/3 | 0,27 | ||||||||
| ОС=0,074 |
Таблица 2.20
Дата добавления: 2021-03-18; просмотров: 522;











