Шаг 2. Нахождение сторон четырехугольника.
Чтобы найди длины сторон полученного четырехугольника, необходимо для каждой из них рассмотреть плоскость грани призмы, в которой она лежит.
| | I способ:
Рассмотрим 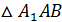 ( ( 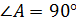 ). По теореме Пифагора: ). По теореме Пифагора:
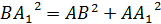
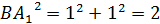
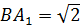
|
II способ:
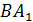 – диагональ квадрата. Поэтому можно воспользоваться формулой: – диагональ квадрата. Поэтому можно воспользоваться формулой:
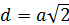
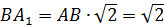
| |
|
|
I способ:
Рассмотрим 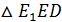 ( ( 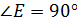 ). По теореме Пифагора: ). По теореме Пифагора:
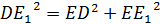
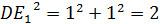
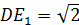
|
II способ:
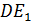 – диагональ квадрата. Поэтому можно воспользоваться формулой: – диагональ квадрата. Поэтому можно воспользоваться формулой:
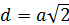
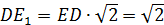
| |
|
|
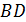 – малая диагональ правильного шестиугольника – малая диагональ правильного шестиугольника 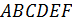 . Поэтому можно воспользоваться фор- мулой: . Поэтому можно воспользоваться фор- мулой:
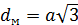
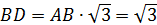
|
| |
 – малая диагональ правильного шестиугольника – малая диагональ правильного шестиугольника  . Поэтому можно воспользоваться формулой: . Поэтому можно воспользоваться формулой:
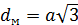
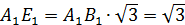
|
Т. о. четырехугольник 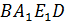 имеетпопарно параллельные и попарно равныестороны. Следовательно,
имеетпопарно параллельные и попарно равныестороны. Следовательно, 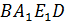 – параллелограмм.Прежде, чем искать площадь сечения, докажем, что данный параллелограмм – прямоугольник. Для этого воспользуемся определением прямоугольника или одним из его свойств.
– параллелограмм.Прежде, чем искать площадь сечения, докажем, что данный параллелограмм – прямоугольник. Для этого воспользуемся определением прямоугольника или одним из его свойств.
Определение: Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойство (признак прямоугольника): Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
I способ:
Докажем, что в параллелограмме 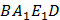 угол
угол 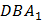 равен
равен  .
.
Плоскости 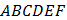 (нижнее основание призмы) и
(нижнее основание призмы) и 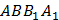 (боковая грань призмы) – перпендикулярные плоскости, пересекающиеся по прямой
(боковая грань призмы) – перпендикулярные плоскости, пересекающиеся по прямой 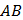 . Прямая
. Прямая 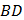 , принадлежащая плоскости
, принадлежащая плоскости 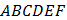 , перпендикулярна прямой пересечения
, перпендикулярна прямой пересечения 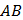 (по свойству малой диагонали правильного шестиугольника).
(по свойству малой диагонали правильного шестиугольника).
Следовательно, прямая 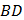 перпендикулярна всей плоскости
перпендикулярна всей плоскости 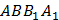 . А если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости. Значит,
. А если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости. Значит, 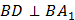 и угол
и угол 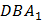 равен
равен  , и параллелограмм
, и параллелограмм 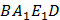 является прямоугольником.
является прямоугольником.
II способ:
Диагоналями параллелограмма 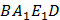 являются отрезки
являются отрезки 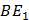 и
и 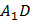 . Докажем, что
. Докажем, что 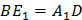 . Для этого найдем длину каждой из диагоналей.
. Для этого найдем длину каждой из диагоналей.
Рассмотрим 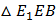 . Бокове ребро
. Бокове ребро 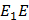 перпендикулярно плоскости основания призмы (по свойству фигуры), а, следовательно, и любой прямой, лежащей в этой плоскости. Значит,
перпендикулярно плоскости основания призмы (по свойству фигуры), а, следовательно, и любой прямой, лежащей в этой плоскости. Значит,  . Таким образом,
. Таким образом, 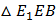 – прямоугольный.
– прямоугольный.
По теореме Пифагора:
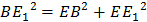
 (как ребро призмы),
(как ребро призмы), 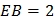 (как большая диагональ правильного шестиугольника).
(как большая диагональ правильного шестиугольника).
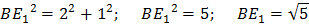
Рассмотрим 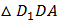 . Бокове ребро
. Бокове ребро 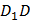 перпендикулярно плоскости основания призмы (по свойству фигуры), а, следовательно, и любой прямой, лежащей в этой плоскости. Значит,
перпендикулярно плоскости основания призмы (по свойству фигуры), а, следовательно, и любой прямой, лежащей в этой плоскости. Значит, 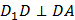 . Таким образом,
. Таким образом, 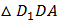 – прямоугольный.
– прямоугольный.
По теореме Пифагора:
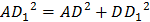
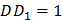 (как ребро призмы),
(как ребро призмы), 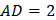 (как большая диагональ правильного шестиугольника).
(как большая диагональ правильного шестиугольника).
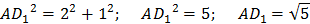
Т.к. 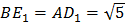 , то параллелограмм
, то параллелограмм 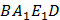 является прямоугольником.
является прямоугольником.
Дата добавления: 2016-12-16; просмотров: 3968;











