ПРАВИЛЬНАЯ ШЕСТУГОЛЬНАЯ ПРИЗМА.
ПОСТРОЕНИЕ ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКА
НА ПЛОСКОСТИ С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ
| Шаг 1: Проведите горизонтальную прямую и отметьте на ней точку. | |
Шаг 2: Возьмите циркуль и проведите окружность произвольного радиуса с центром в точке 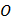 . Точки пересечения окружности с прямой обозначьте . Точки пересечения окружности с прямой обозначьте 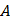 и и 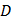 соответственно. соответственно.
| |
Шаг 3: Установите ножку циркуля в точку 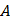 и проведите вторую окружность такого же радиуса. Окружность должна пройти через точку и проведите вторую окружность такого же радиуса. Окружность должна пройти через точку 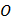 . Обозначьте точки пересечения окружностей . Обозначьте точки пересечения окружностей 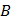 и и 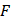 соответственно. соответственно.
| |
Шаг 4: Установите ножку циркуля в точку 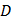 и проведите третью окружность такого же радиуса. Окружность должна пройти через точку и проведите третью окружность такого же радиуса. Окружность должна пройти через точку 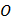 . Обозначьте точки пересечения с первой окружностью . Обозначьте точки пересечения с первой окружностью 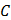 и и 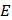 соответственно. соответственно.
| |
Шаг 5: Последовательно соедините точки 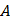 , , 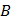 , , 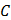 , , 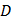 , , 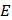 и и 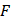 отрезками. Полученный шестиугольник является правильным. отрезками. Полученный шестиугольник является правильным.
| |
ЧАСТЬ 2.
ПРАВИЛЬНАЯ ШЕСТУГОЛЬНАЯ ПРИЗМА.
ПОСТРОЕНИЕ.
Df:Призма называется правильной, если в основании ее лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания.В основании правильной шестиугольной призмы лежит правильный шестиугольник.
Свойство 1:Боковое ребро правильной призмы перпендикулярно любой прямой, расположенной в плоскости нижнего (верхнего) основания.
Свойство 2:Боковые грани правильной шестиугольной призмы – прямоугольники.При определенных условиях задачи могут быть квадратами.
Свойство 3: Боковые грани призмы, проходящие через противоположные стороны основания, параллельны.
ПОСТРОЕНИЕ ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ
ПРИЗМЫ НА ПЛОСКОСТИ
Вариант 1.
| Шаг 1 | Шаг 2 | Шаг 3 |
| | | |
| Шаг 4 | Шаг 5 | Шаг 6 |
| | | |
| Шаг 7 | Шаг 8 | Шаг 9 |
| | | |
Вариант 2.
| Шаг 1 | Шаг 2 | Шаг 3 |
| | | |
| Шаг 4 | Шаг 5 | Шаг 6 |
| | | |
| Шаг 7 | Шаг 8 | Шаг 9 |
| | | |
ЧАСТЬ 3.
ПРАВИЛЬНАЯ ШЕСТУГОЛЬНАЯ ПРИЗМА.
Дата добавления: 2016-12-16; просмотров: 2503;











