Решение. Шаг 1. Построение сечения
| Строим призму и отмечаем на ней точки, через которые, по условию, проходит сечение. | |
| Среди этих точек находим пары тех, которые лежат в одной плоскости, и соединяем их отрезками. | |
Далее строим сечение (замкнутую ломаную), пользуясь свойством параллельности: если каждая из пересекающихся плоскостей проходит через одну из двух параллельных прямых, то прямая пересечения плоскостей параллельна этим прямым. В нашем случае это означает, что т.к. плоскости
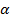 (сечение, которое мы строим) и
(сечение, которое мы строим) и 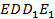 (задняя грань призмы) проходят через параллельные прямые (плоскость
(задняя грань призмы) проходят через параллельные прямые (плоскость 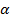 проходит через прямую
проходит через прямую 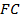 , плоскость
, плоскость 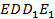 проходит через прямую
проходит через прямую 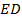 , и прямая
, и прямая 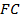 параллельна прямой
параллельна прямой 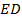 по свойству большой диагонали правильного шестиугольника), то прямая пересечения этих плоскостей, проходящая через точку
по свойству большой диагонали правильного шестиугольника), то прямая пересечения этих плоскостей, проходящая через точку 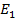 , должна быть параллельна этим двум прямым. Такой прямой будет прямая
, должна быть параллельна этим двум прямым. Такой прямой будет прямая 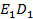 .
.
Т. о. точка 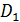 – дополнительная точка, принадлежащая плоскости искомого сечения.
Ребро призмы – дополнительная точка, принадлежащая плоскости искомого сечения.
Ребро призмы 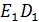 также будет частью замкнутой ломаной, которую мы строим. также будет частью замкнутой ломаной, которую мы строим.
| |
Точки 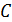 и и 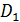 лежат в плоскости боковой грани призмы лежат в плоскости боковой грани призмы 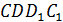 , поэтому мы можем соединить их отрезком.
Полученный отрезок , поэтому мы можем соединить их отрезком.
Полученный отрезок 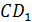 также будет частью замкнутой ломаной, которую мы строим. также будет частью замкнутой ломаной, которую мы строим.
| |
Полученный в результате построенийчетырехугольник 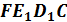 будетискомым сечением.Т.к. две стороны этого четырехугольника параллельны (
будетискомым сечением.Т.к. две стороны этого четырехугольника параллельны ( 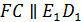 ), а две – не параллельны (
), а две – не параллельны ( 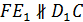 ), то
), то 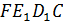 – трапеция.
– трапеция.
Дата добавления: 2016-12-16; просмотров: 1912;











