ПОСТРОЕНИЕ СЕЧЕНИЙ.

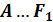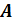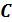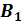1. Изобразите сечение правильной шестиугольной призмы , все ребра которой равны 1, проходящее через вершины , и . Найдите его площадь.

Решение. Шаг 1. Построение сечения

Строим призму и отмечаем на ней точки, через которые, по условию, проходит сечение.
Среди этих точек находим пары тех, которые лежат в одной плоскости, и соединяем их отрезками.

Полученный в результате построенийтреугольник 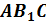будетискомым сечением.

Шаг 2. Нахождение сторон треугольника.

Чтобы найди длины сторон полученного треугольника, необходимо для каждой из них рассмотреть плоскость грани призмы, в которой она лежит.

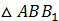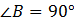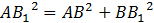
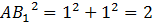
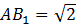	I способ: Рассмотрим ( ). По теореме Пифагора: II способ: 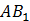– диагональ квадрата. Поэтому можно воспользоваться формулой:
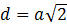
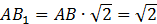
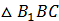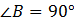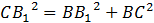
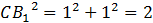
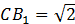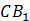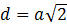
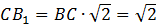
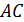	I способ: Рассмотрим ( ). По теореме Пифагора: II способ: – диагональ квадрата. Поэтому можно воспользоваться формулой:
	– малая диагональ правильного шестиугольника. Поэтому можно воспользоваться формулой:

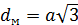
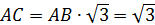
Дата добавления: 2016-12-16; просмотров: 2377;