Прогнозирование экономических процессов

Прогнозирование представляет собой научное выявление состояния и вероятных путей развития явлений и процессов, основанное на системе установленных причинно–следственных связей и закономерностей. Прогнозирование предполагает оценку показателей, характеризующих эти явления и процессы, для будущего.

Прогнозирование распространяется на такие процессы, управление которыми в момент выработки прогноза либо возможно в весьма малом диапазоне, либо совсем невозможно, либо оно возможно, но требует учета действия таких факторов, влияние которых не может быть полностью или однозначно определено. Прогнозы экономических явлений и процессов разрабатываются в виде качественных характеристик развития и количественных оценок прогнозируемых показателей. Качественные характеристики дают общее описание тенденции и ожидаемого характера изменений, а в самом простом случае – утверждение о возможности или невозможности наступления какого–либо события. Количественные оценки могут быть точечными и интервальными и сопровождаются определением вероятностей достижения величины прогнозируемого показателя. Правильность исходных теоретических предпосылок и методологической основы прогноза решающим образом влияет на его результаты и возможность их практического использования.

Составление прогнозов, как правило, предшествует процессу планирования и служит для него исходной базой.

В планировании используется система прогнозов: демографических, социальных, экономических, научно–технического прогресса, природных ресурсов и др.

Точечный прогноз дается в виде единственного значения прогнозируемой величины.

Интервальный прогнозохватывает совокупность значений прогнозируемой величины. Чем шире интервальный прогноз, тем выше вероятность осуществления прогноза (надежность прогноза), но меньше его априорная точность. Интервальный прогноз чаще всего определяется на основе расчета доверительных границ прогноза и учитывает лишь ту неопределенность, которая связана с ошибками параметров прогнозной модели и принятой степенью надежности прогноза. Интервальные прогнозы y определяются на основе точечного прогноза следующим образом:

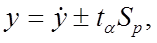
где 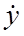– точечный прогноз; – значение t –статистики Стьюдента; S_p – средняя квадратическая ошибка прогноза.

Значения S_p для наиболее употребительных прогнозных моделей определяются следующим образом (табл.3.4):

Таблица 3.4

Средняя квадратическая ошибка прогноза

Прогнозная модель	Формула для расчета Sp
Средняя     Экспоненциальная средняя (для стационарного ряда)     Линейный тренд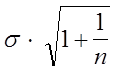

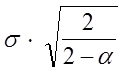
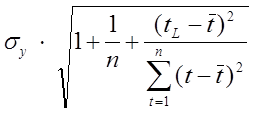
где 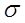– среднее квадратическое отклонение прогнозируемой величины (по данным наблюдений); n – число наблюдений; 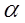– коэффициент сглаживания; 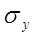– среднее квадратическое отклонение фактических наблюдений от расчетных; t – порядковый номер в ряду, t = 1, . . . n ; t_L – время, для которого делается экстраполяция, т.е. t_L = n + L; 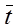– среднее значение времени,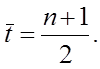

Экстраполяцией называется нахождение значений показателя за пределами области определения ряда динамики. Экстраполяция может быть перспективной и ретроспективной. Перспективная экстраполяция (прогнозирование) – продолжение уровней ряда в будущее. Ретроспективная экстраполяция – продолжение уровней ряда в прошлое. При анализе рядов динамики может

возникать необходимость определения промежуточных значений (интерполяция) уровней ряда в области его определения.

Эмпирической мерой точности прогноза служит величина его ошибки – абсолютная или относительная разность между фактическим значением (реализацией прогноза) и точечным прогнозом. Обобщающими характеристиками точности могут служить средняя или медианная погрешность, средняя квадратическая ошибка прогноза, коэффициент несоответствия.

Коэффициент несоответствия определяется следующим образом:

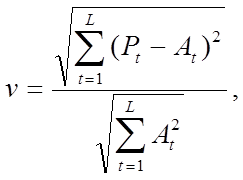
где P_t и A_t – прогнозное и фактическое (реализованное) изменения показателя (приросты).

Коэффициент v = 0, когда фактические изменения равны предсказанным; v = 1, когда процесс прогнозирования приводит к такой же средней квадратической ошибке, что и “наивная” экстраполяция неизменности; v > 1, когда прогноз дает худшие результаты, чем предположение о неизменности исследуемого явления. Верхней границы коэффициент не имеет.

Интервальный прогноз считается оправдавшимся, если фактическое значение показателя попадает в этот интервал. Обобщающей характеристикой точности серии интервальных прогнозов может служить относительное число оправдавшихся прогнозов в общем их числе.

Априорной мерой точности при разработке прогноза служит дисперсия применяемой прогнозной модели, например, дисперсия выборочной, скользящей и экспоненциальной средней, дисперсия тренда, уравнения регрессии и т.д. Модель, дающая более узкий доверительный интервал при всех прочих равных условиях, рассматривается как более точный инструмент прогноза.