Алгоритм построения

1. Задать проекции элементов определителя: построить цилиндрическую винтовую линию из 12 точек (рис. 2-112);

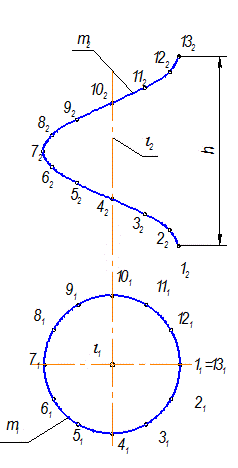
Проекции элементов определителя наклонного геликоида

Рис. 2-112

Задать проекции направляющего конуса (провести 12 образующих) (рис. 2-111), наклон образующих которого к оси определит угол наклона образующих геликоида. Углы j у образующих конуса (1₂¹) и геликоида (1₂) не искажаются, т. к. эти образующие занимают положение фронтали.

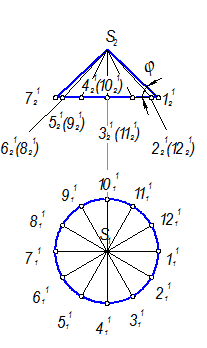
Проекции направляющего конуса

Рис. 2-111

2. Построение геликоида начинаем с горизонтальной проекции. Из точек 1₁ и 2₁ провести образующие геликоида параллельно соответствующим образующим конуса 1₁¹ и 2₁¹ до пересечения с осью – i₁ (рис. 2-113).

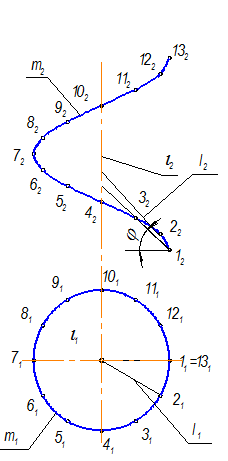
Рис. 2-113

3. На фронтальной проекции из точек 1₂ и 2₂ провести образующие геликоида параллельно соответствующим образующим конуса 1₂¹ и 2₂¹ до пересечения с осью – i₂.

4. Остальные образующие геликоида строить таким же образом

Направляющий конус может быть соосным с наклонным геликоидом (рис. 2-114)

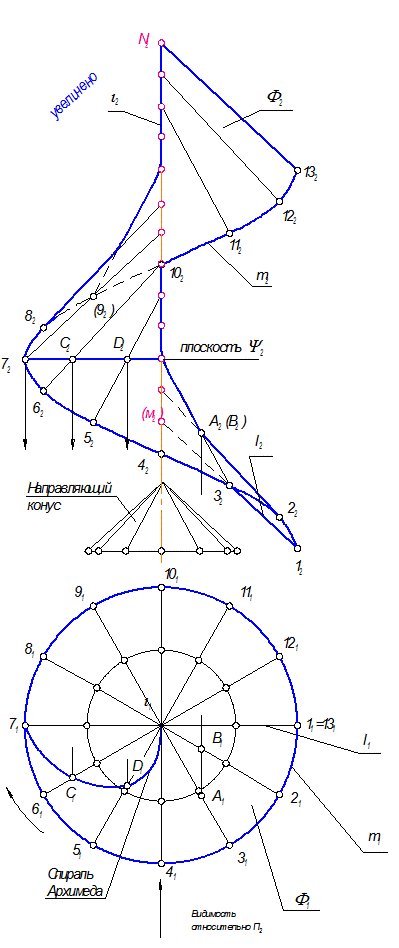
Рис. 2-114

5. Определить видимость поверхности, как всегда, с помощью конкурирующих точек, например выбрать фронтально конкурирующие А₂ = В₂, т.е. образующая 3₂ закрывает образующую 2₂, направляющая и образующие от точки 8 до точки 10 - невидимы.

6. Обвести проекции поверхности на П₂ с учетом видимости. Очертание геликоида на фронтальной проекции получается как огибающая семейство прямолинейных образующих.

7. В сечении геликоида плоскостью Y(Y₂), перпендикулярной ее оси, получается спираль Архимеда.

Каркас образующих наклонного геликоида можно построить и без применения направляющего конуса.

Образующие 1₂М₂ и 13₂N₂ || П₂, т.е. занимают положение фронталей, поэтому при заданном угле наклона образующей геликоида сразу определяют положение точек М₂ и N₂.

Расстояние (шаг) между этими точками делят на 12 равных частей и соединяют с соответствующими точками на цилиндрической винтовой направляющей.

Контрольные вопросы

1. Что означает "кинематический принцип образования поверхности"?

2. Что называется определителем поверхности?

3. Какие поверхности называются линейчатыми?

4. Сформулируйте признак принадлежности точки поверхности.

5. Перечислите поверхности вращения второго порядка.

6. Назовите поверхности с плоскостью параллелизма.

7. Какие поверхности могут занимать проецирующее положение?

Ответы на тест - № 4

1-5 2-3 3-6 4-2 5-6 6-1 7-5 8-6