Е уравнение Максвелла

Теорема Остроградского-Гаусса применительно к магнитным полям:

,

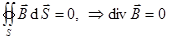так как не существует магнитных зарядов.

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

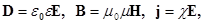
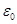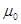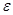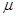где и - соответственно электрическая и магнитная постоянные, и - соответственно диэлектрическая и магнитная проницаемости, 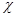- удельная проводимость вещества.

Недостаток уравнений Максвелла: уравнения не описывают, откуда и как берутся поля.

Из уравнений Максвелла следует существование электромагнитных волн, которые распространяются в вакууме со скоростью света:

.

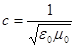Волновое уравнение

Рассмотрим нейтральную ( 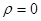), непроводящую ( 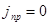) с 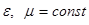изотропную среду:

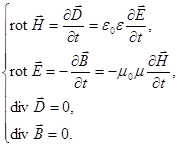
тогда, учитывая, что 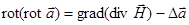, получаем:

,

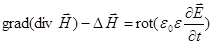тогда так как 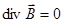, то 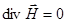и окончательное уравнение:

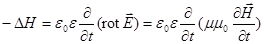, или же

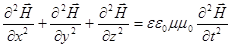- волновое уравнение.

Решение этого уравнения: 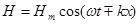, где 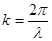- волновое число, 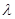- длина волны, “-” соответствует положительному направлению распространения, “+” соответствует обратному направлению распространения (против оси ).

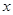Геометрическое место точек, за которое доходит волна за одно и то же время, называется волновой поверхностью.

Граница между областью, где есть колебания и нет, называется фронтом волны (по сути, передняя волновая поверхность).

По виду фронта различают сферические, цилиндрические и плоские волны. Причем любой волновой процесс можно представить в виде суперпозиции плоских волн.