Закон сохранения и превращения энергии

Закон сохранения и превращения энергии в механике

В 1748 году М.В. Ломоносов впервые сформулировал закон сохранения и превращения энергии. Спустя сто лет Р. Майер и Г. Гельмгольц дали количественную формулировку закона сохранения и превращения энергии, который состоит в следующем: в замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но ее общее количество остается неизменным.

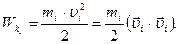Найдем условие, которому должна удовлетворять система тел для того, чтобы ее полная механическая энергия не изменялась с течением времени. Если - скорость i –ой материальной точки системы массой m_i, то ее кинетическая энергия может быть представлена в виде: Изменение этой энергии за малый промежуток времени dt, связанное с изменением скорости 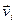на ( 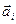- ускорение i-ой материальной точки), равно

dW_ki =W_ki(t₂)-W_ki(t₁),

где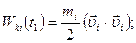

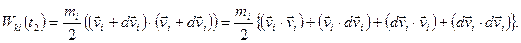
С учетом того, что 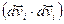- величина второго порядка малости, можно получить:

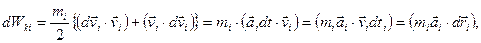
(3.3.1,а)

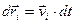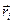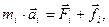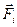где - приращение радиуса-вектора материальной точки. По второму закону Ньютона где и 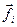- результирующие консервативных и неконсервативных сил, соответственно, действующих на i-ую материальную точку. Поэтому

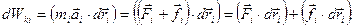
(3.3.1,б)

Кинетическая энергия всей системы равна сумме кинетических энергий всех материальных точек, образующих эту систему, а ее изменение за малый промежуток времени dt:

или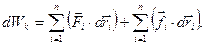

Первая сумма в правой части последнего выражения представляет собой суммарную работу , совершаемую всеми консервативными силами за промежуток времени dt. Согласно уравнению (3.2.6,б), работа равна убыли потенциальной энергии системы за время dt, то есть 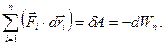Вторая сумма в вышеприведенном выражении представляет собой работу, совершаемую всеми неконсервативными силами: Таким образом,

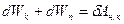
(3.3.2,а)

или

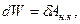
(3.3.2,б)

где W = W_к + W_п - полная механическая энергия системы (3.2.10).

Консервативной системой называют систему тел (материальных точек), внутренние силы взаимодействия между которыми – консервативны, а все внешние силы – стационарны (стационарные силы – силы, которые могут изменяться с течением времени только вследствие изменения положения системы отсчета) и консервативны. Для консервативной системы работа неконсервативных сил равна нулю 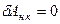и, как следствие, W = W_к + W_п = const, то есть полная механическая энергия консервативной системы не изменяется с течением времени – закон сохранения механической энергии. Вышеуказанный закон справедлив, в частности, для замкнутой консервативной системы, то есть системы, на которую внешние силы вообще не действуют, а все внутренние силы – консервативны.

Рассмотрим применение закона сохранения механической энергии при расчете абсолютно упругого прямого удара двух тел (рис. 3.7.).

Абсолютно упругим ударом называют такой удар, в результате которого не происходит превращения механической энергии системы соударяющихся тел в другие виды энергии.

Пусть два абсолютно упругих шара массами m₁ и m₂ до удара движутся поступательно со скоростями и 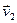, направленными в одну и ту же сторону вдоль линии их центров, причем > 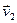. Задача: Необходимо определить скорости шаров после соударения: 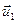и .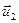

В процессе удара систему соударяющихся тел можно считать замкнутой. При абсолютно упругом ударе система консервативна. В этом случае для решения задачи можно использовать законы сохранения механической энергии и импульса. Перед ударом и после него тела не деформированы, то есть потенциальную энергию системы в этих двух состояниях можно считать одинаковой и равной нулю. Следовательно,

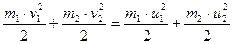
(3.3.3)

и

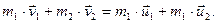
(3.3.4,а)

При прямом центральном ударе векторы скоростей шаров до и после удара направлены вдоль одной прямой – линии удара. Поэтому (3.3.4,а) можно переписать в виде:

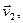
где v₁, v₂, u₁ и u₂ – проекции векторов 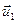и 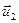на ось координат, параллельную линии удара. После несложных преобразований уравнений (3.3.3) и (3.3.4,б) можно получить:

(3.3.5)

Следует помнить, что в (3.3.5) скорости v₁ и v₂ могут иметь как одинаковые, так и противоположные знаки, в зависимости от направления векторов и 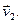Рассмотрим некоторые частные случаи:

1) массы шаров одинаковы (m₁ = m₂ = m). При этом u₁ = v₂, u₂ = v₁, то есть при ударе шары обмениваются скоростями;

2) масса второго шара во много раз больше массы первого (m₂ » m₁). В этом случае u₁ @ 2v₂ - v₁; u₂ = v₂. Если при этом второй шар до удара был неподвижен, то u₁ = - v₁ u₂ = 0, то есть первый шар отскакивает от неподвижного второго шара и движется в обратную сторону со скоростью

Равновесие системы

На основе закона сохранения механической энергии замкнутой консервативной системы можно рассмотреть вопрос о равновесии системы. Говорят, что система тел находится в равновесии, если она может быть выведена из этого состояния только в результате внешнего воздействия. Например, система Земля – тело находится в равновесии, если тело неподвижно лежит на дне ямы или на горизонтальной вершине горы. Состояние равновесия называется устойчивым,если малое внешнее воздействие на систему вызывает малое изменение ее состояния (пример – тело лежит на дне ямы). При этом в системе возникают внутренние силы, стремящиеся возвратить систему в прежнее состояние. Состояние равновесия называется неустойчивым (лабильным), если даже при сколь угодно малом внешнем воздействии система выводится из этого состояния (пример - тело находится у края пропасти, и при малом воздействии падает вниз, и не возвращается в первоначальное состояние неустойчивого равновесия).

Рассмотрим замкнутую систему Земля и шар, находящийся на различных участках горной цепи A, B, C, D (на различных высотах y) (рис. 3.8). Легко видеть, что положение B шара соответствует неустойчивому (лабильному) равновесию, а C, D – устойчивому. Для того чтобы, например, выкатить шар из ямы D, необходимо совершить работу внешних сил, которая равна разности потенциальной энергии шара в положениях B и D: A = W_пB – W_пD. Чем глубже яма D (или C) (рис. 3.8), тем большую работу А против силы тяжести необходимо произвести для поднятия шара из этой “потенциальной ямы”- положения устойчивого равновесия. Таким образом, в состоянии устойчивого равновесия замкнутая система обладает минимумом (локальным или абсолютным) потенциальной энергии. В состоянии неустойчивого равновесия – максимумом потенциальной энергии. Наиболее устойчивому состоянию системы соответствует абсолютный минимум ее потенциальной энергии, то
есть наименьшее из всех возможных значений ее потенциальной энергии (положение D (рис. 3.8)).

Положение D соответствует абсолютному минимуму энергии – это положение стабильного равновесия. Если шар в состоянии C (рис. 3.8) приобретет энергию (над ним совершат работу внешние силы) A = W_пB – W_пС., то он перейдет в состояние D – стабильного равновесия. Поэтому состояние системы в положении С называют метастабильным равновесием. Энергия системы в положении А (рис. 3.8) при бесконечно малом отклонении шара от своего положения не меняется – это положение безразличного равновесия.

Связь потенциальной энергии с потенциальными силами позволяет задавать воздействие потенциальных сил на тело зависимостью потенциальной энергии от координат, например для одномерного случая Е_n=f(x). Кривые, соответствующие этой зависимости называются потенциальными кривыми (рис.3.9).

В случае устойчивого равновесия можно указать некоторую ограниченную область пространства (рис.3.9. (1), область сd), в которой потенциальная энергия меньше, чем вне ее. Эта область получила название потенциальной ямы.