Глава 3. Энергия и работа

Работа и мощность

Работа силы в поступательном движении

В жизни человека работа и энергия играют исключительно важную роль. Обе эти величины тесно связаны между собой. В физике под работой понимают физическую величину, характеризующую действие силы на определенном пути. В простейшем случае, когда постоянная сила F, направленная вдоль пути l, действует на прямолинейно движущееся тело, работу A можно определить следующим образом:

При равенстве нулю одного из сомножителей в (3.1.1) (нет силы или нет пути) равна нулю и работа. В частности, если сила F поддерживает в равновесии неподвижный груз в поле тяжести, то ее работа равна нулю. Даже, если тело движется горизонтально (рис. 3.1.), то сила F по-прежнему удерживает тело от падения и, следовательно, на этом пути ее работа равна нулю.

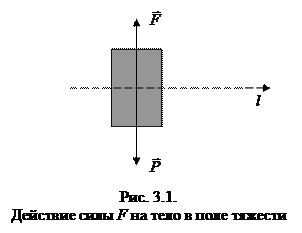В общем случае, сила, перпендикулярная пути, на этом пути работы не совершает. Пусть теперь постоянная сила действует на прямолинейном пути l под углом a к нему. Работу силы можно представить как сумму работ ее составляющих (проекций), направленных параллельно и перпендикулярно пути (рис. 3.2).

Выше отмечалось, что работа перпендикулярной составляющей равна нулю. Следовательно, работа заданной силы равна работе, совершаемой под действием продольной составляющей силы:

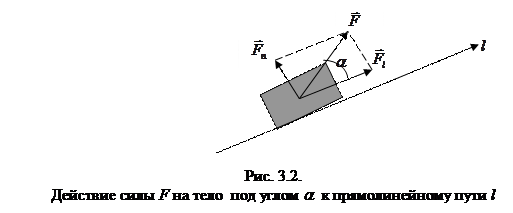Величина работы в (3.1.2) положительна, если направления продольной составляющей силы и пути совпадают (a < 90°, cosa > 0), и в этом случае силу называют движущей. Когда величина работы отрицательна, силу называют силой сопротивления. В общем случае тело может двигаться произвольным, достаточно сложным образом, а сила 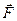- изменяться так, что формулой (3.1.2) пользоваться нельзя. Однако, рассматривая достаточно малое (элементарное) перемещение тела, можно считать силу постоянной 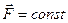, а движение точки ее приложения – прямолинейным. Поэтому, элементарной работой, совершаемой произвольной силой 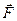при перемещении точки ее приложения на малое расстояние dl, называют величину:

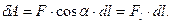
(3.1.3,а)

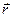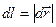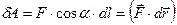Если - радиус-вектор точки приложения силы, то и - элементарная работа соответствует скалярному произведению векторов силы 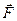и элементарного перемещения 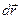точки ее приложения. Нетрудно видеть, что:

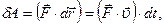
(3.1.3,б)

где 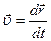- скорость точки приложения силы.

Работа, совершаемая силой 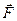на конечном пути l, равна сумме элементарных работ на отдельных бесконечно малых участках пути, то есть

(3.1.4,а)

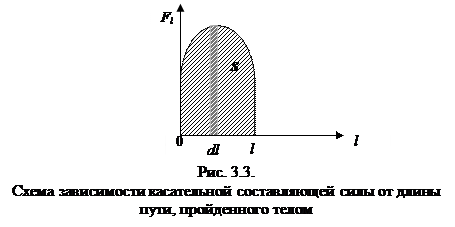Если величина F_l - касательной составляющей силы 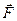, задана как функция от длины пути l (рис. 3.3), то, как видно из уравнения (3.1.4,а), работа A, совершаемая силой 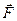на пути l, измеряется площадью фигуры, заштрихованной на рис. 3.3. Если не зависит от l ( ), то

В случае, когда 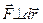, сила лишь искривляет траекторию движущегося тела, но работу не совершает. В качестве примера можно указать на работы центростремительной силы при действии на материальную точку, равномерно движущуюся по окружности.

Если на материальную точку одновременно действуют n сил 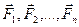то алгебраическая сумма работ, совершаемых всеми этими силами на малом перемещении 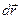материальной точки, равна работе, совершаемой на том же перемещении результирующей силой :

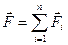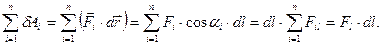
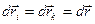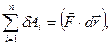Если тело - абсолютно твердое, и оно движется поступательно, то перемещение всех точек тела за время dt одинаковы: и где 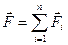- главный вектор внешних сил, приложенных к телу.

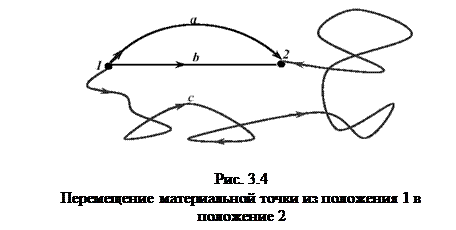
Силу 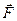, действующую на материальную точку, называют консервативной, или потенциальной, если работа A_1-2, совершаемая этой силой при перемещении точки из одного произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло: A_1-a-2 = A_1-b-2 = А_1-с-2= A_1-2, где A_1-a-2 – работа силы при перемещении точки из положения 1 в 2 по траектории 1-а-2, A_1-b-2 – работа силы вдоль траектории 1-b-2; А_1-с-2 – работа силы при перемещении вдоль траектории 1-с-2 (см. рис. 3.4).

Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака работы консервативной силы, так как величина F_l в выражении (3.1.4,а) меняет свой знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории L работа консервативной силы тождественно равна нулю:

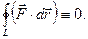
(3.1.4,б)

Из выражения (3.1.4,б) следует, что подинтегральное выражение 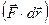(элементарная работа консервативных сил) представляет собой полный дифференциал функции координат. Примерами консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия между заряженными телами.

Все силы, не удовлетворяющие условию (3.1.4,б), называют неконсервативными. Характерным примером таких сил являются силы трения (например, при скольжении, движении в вязкой среде и так далее). Сила трения всегда направлена в сторону, противоположную направлению движения (на рис. 3.2. cosa = -1). Поэтому работа силы трения при перемещении точки ее приложения вдоль замкнутой траектории всегда отрицательна и никогда не равна нулю.

В международной системе единиц измерения СИ единицей работы является один джоуль (1 Дж) – такая работа, которая совершается силой 1 Н на пути длиной 1 м в направлении действия силы.

Мощность силы в поступательном движении

Для характеристики скорости совершения работы силой вводится понятие мощности. Мощностью N силы 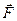называется физическая величина, численно равная работе, совершаемой этой силой за единицу времени:

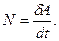
(3.1.5)

Используя выражение (3.1.3,а), уравнение (3.1.5) может быть представлено в виде

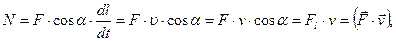
(3.1.6,а)

где 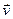- скорость точки приложения силы, 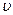- путевая скорость точки приложения силы. Следовательно, мощность (или мгновенная мощность) силы равна произведению численных значений касательной составляющей силы и скорости движения, то есть скалярному произведению векторов силы и скорости. Если мощность N ¹ const, то часто пользуются средней мощностью N_ср за некоторый конечный промежуток времени t, в течении которого сила совершила работу A:

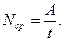
(3.1.6,б)

Единицей измерения мощности в системе СИ является ватт – Вт.

Работа силы во вращательном движении

Согласно выражению (3.1.3,а), элементарная работа силы, действующей на i-ую материальную точку тела, вращающегося относительно неподвижной оси OZ, может представлена в виде: 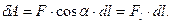Учтем, что за малый промежуток времени dt путь, пройденный материальной точкой dl, представляет собой длину дуги окружности, по которой движется точка: dl = r×dj, где r - радиус окружности; dj - угол поворота тела за время dt. Следовательно, 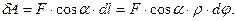С другой стороны, из определения момента силы при движении тела вокруг закрепленной оси 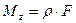. Таким образом, с учетом определения скалярного произведения векторов:

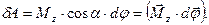
(3.1.7)

Работа, совершаемая за конечный промежуток времени при вращательном движении, равна

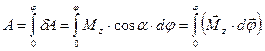
(3.1.8)

Мощность силы во вращательном движении

При подстановке уравнения (3.1.7) в выражение (3.1.5) получим, что мощность силы во вращательном движении можно найти из следующего выражения:

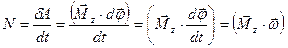
(3.1.9)