Моменты системы случайных величин

<4 5 678 9 10 >

Начальным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения X^k на Y^s:

α_k_,_s = M [X^kY^s]. (3.4)

Центральным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения k-й и s-й степени соответствующих центрированных величин:

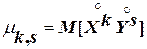, (3.5)

где .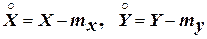

Выпишем формулы, служащие для непосредственного подсчета моментов. Для дискретных случайных величин:

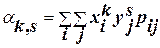(3.6)

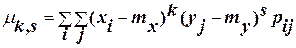, (3.7)

где p_i _j = P((X = x_i )(Y = y_j )) есть вероятность того, что система (X, Y) примет значение (x_i , y_j ), а суммирование распространяется по всем возможным значениям случайных величин X, Y.

Для непрерывных случайных величин:

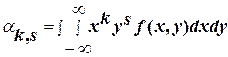, (3.8)

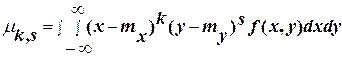, (3.9)

где f(x,y) – плотность распределения системы.

Первые начальные моменты представляют собой уже известные нам математические ожидания величин X и Y, входящих в систему:

m_x= α_1,0= M[X¹Y⁰] = M[X],

m_y= α_0,1= M[X⁰Y¹] = M[Y].

Совокупность математических ожиданий m_x и m_y представляет собой характеристику положения системы. Геометрически это координаты средней точки на плоскости, вокруг которой происходит рассеивание точки (X, Y).

Кроме первых начальных моментов, на практике широко применяются еще вторые центральные моменты системы. Два из них представляют собой дисперсии величин X и Y

,

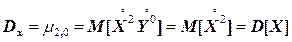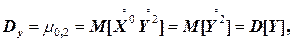
характеризующие рассеивание случайной точки в направлении осей Ox и Oy.

Особую роль как характеристики системы играет второй смешанный центральный момент

,

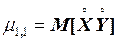т.е. математическое ожидание произведения центрированных величин.

Ввиду того, что этот момент играет важную роль в теории систем случайных величин, введем для него особое обозначение:

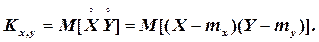(3.10)

Характеристика K_х,уназывается корреляционным моментом (иначе – «моментом связи») случайных величин X и Y.

Для прерывных случайных величин корреляционный момент выражается формулой

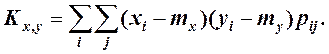, (3.11)

а для непрерывных – формулой

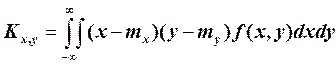(3.12)

Таким образом, если корреляционный момент двух случайных величин отличен от нуля, это есть признак наличия зависимости между ними.

Из формулы (3.10) видно, что корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Действительно, если, например, одна из величин (X, Y) весьма мало отклоняется от своего математического ожидания (почти не случайна), то корреляционный момент будет мал, какой бы тесной зависимостью ни были связаны величины (X, Y). Поэтому для характеристики связи между величинами (X, Y) в чистом виде переходят от момента к безразмерной характеристике

, (3.13)

где 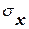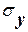– средние квадратические отклонения величин X и Y. Эта характеристика называется коэффициентом корреляции величин X и Y. Очевидно, коэффициент корреляции обращается в нуль одновременно с корреляционным моментом; следовательно, для независимых случайных величин коэффициент корреляции равен нулю.

Случайные величины, для которых корреляционный момент (а значит, и коэффициент корреляции) равен нулю, называются некоррелированными (иногда – «несвязанными»).

<4 5 678 9 10 >

Дата добавления: 2016-12-09; просмотров: 2180;