Дифференциальное уравнение конвективного теплообмена

В установившемся потоке жидкости выделим элементарный объем (в виде куба) с гранямиdx, dy, dz. Примем, что плотность жидкости r ,ее коэффициент теплопроводности l и удельная теплоемкость С постоянны, а температураt изменяется вдоль граней куба. Проекции скорости движения жидкости W на оси координат x, y, z составляют W_x W_y W_z соответственно. Будем считать, что тепло переносится в жидкости путем конвекции и теплопроводности и затрачивается только на изменение энтальпии куба. Тогда конвективная составляющая теплового потока будет иметь вид:

,

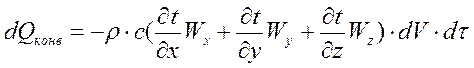где dV – объем куба.

А количество тепла, вносимого в элементарный объем за время t путем теплопроводности, составит

.

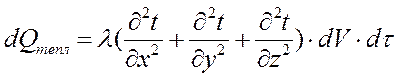Общее количество тепла .dQ, подводимое конвекцией и теплопроводностью

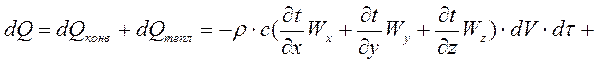
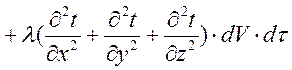(1-9)

Это количество тепла равно соответствующему изменению энтальпии элементарного куба:

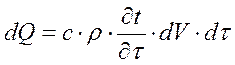(1-10)

Тогда, приравняв выражение (1-9) и (1-10), проведя сокращение и преобразование, получим

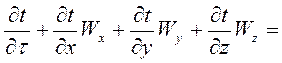
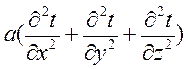(1-11)

где 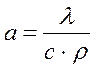- коэффициент температуропроводности.

Выражение (1-11) является дифференциальным уравнением конвективного теплообмена и в общем виде выражает распределение температур в движущейся жидкости. Отметим, что при установившемся процессе теплообмена .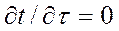

Чтобы получить полное математическое описание процесса уравнение (1-11) необходимо дополнить условиями на границе раздела потока и стенки аппарата. Выше мы рассматривали поток жидкости как двухслойную систему, состоящую из пограничного теплового слоя толщиной δ_тепл. и ядра потока, двигающегося в турбулентном режиме. В пограничном слое теплота от стенки аппарата распространяется теплопроводностью, которая описывается уравнением(1-5). Это же количество теплоты передается ядру потока согласно закону Ньютона по уравнению (1-7). Приравняв выражения(1-5) и (1-7), получим уравнение характеризующее условия на границе:

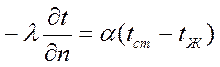(1-12)

Однако выражения (1-11) и (1-12) можно привести к расчетному виду только для простейших случаев. Поэтому обычно используют другой путь, заключающийся в том, что расчетные выражения получают из общих дифференциальных уравнений, применяя методы теории подобия, и приводятих к конкретному виду с помощью экспериментальных данных.

Тепловое подобие

I. Рассмотрим сначала подобие граничных условий. Оно описывается с помощью критерия Нуссельта:

.

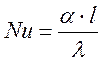Равенство критериев Nuхарактеризует подобие процессов теплопереноса на границе между стенкой и потоком жидкости. Он является мерой соотношения толщины пограничного слоя δ_тепл и определяющего геометрического размера. В критерий входит определяемая в задачах по конвективному теплообмену величина α.

2. Рассмотрим условия подобия в ядре потока. Оно описывается с помощью критерия Фурье, который характеризует связь между скоростью изменения температурного поля, размерами канала, в котором происходит теплообмен, и физическими свойствами среды в нестационарных условиях:

.

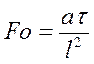Равенство критериев Fo в сходных точках тепловых потоков - необходимое условие подобия неустановившихся процессов теплообмена.

3. Критерий Пеклепоказывает соотношение между количеством тепла, переносимым путем конвекции и теплопроводности при конвективном теплообмене:

.

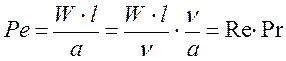4. Критерий Прандтля характеризует поле теплофизических величин потока жидкости:

.

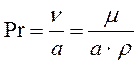5. Критерий Грасгофавводится при теплообмене в условиях естественной конвекции и показывает меру отношения сил трения к подъемной силе, определяемой разностью плотностей в различных точках потока:

.

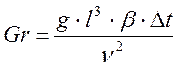гдеβ - коэффициент объемного расширения жидкости, град^-1; Δt- разность температур горячих и холодных частиц жидкости, вызывающих естественную конвекцию, град.

Необходимыми условиями подобия переноса тепла является соблюдение гидродинамического и геометрического подобия. Первое характеризуется равенством критериев Re в сходственных точках подобных потоков, второе - постоянством отношения основных геометрических размеров стенки L₁,L₂,…,L_n к некоторому характерному размеру.

Таким образом, критериальное уравнение конвективного теплообмена выражается в виде:

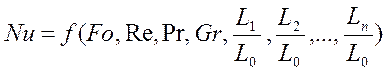. (1-13)

С учетом того, что критерий Nuявляется определяемым, т.к. в него входит искомая величина коэффициента теплоотдачи α. При установившемся процессе теплообмена из выражения (1-13) исключают критерий Fo. При вынужденном установившемся движении влиянием критерия Gr на теплопередачу можно пренебречь. Тогда:

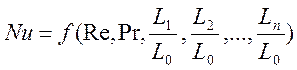. (1-14)

Вид функции (1-14) определяется опытным путем, причем обычноей придают степенную форму. Например, при движении потока в трубе диаметром d и длиной lуравнение (1-14) примет вид:

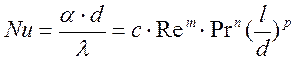, (1-15)

где величины c, m, n, p определяются по опытным данным.

Коэффициент теплоотдачи α определяется по найденному из критериальных уравнений критерию Нуссельта.