Элементы симметрии.


Симметрия – способность твердого тела совмещаться с самим собой в результате его движения или воображаемых операций над ним. Рассмотрим три основных операции симметрии.

1. Ось симметрии n-ого порядка. Если тело совмещается с самим собой при повороте на угол 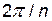вокруг оси, то ось называется осью симметрии n-ого порядка.

2. Плоскость симметрии. Если тело совмещается с самим в результате зеркального отражения его точек в некоторой плоскости, то эта плоскость называется плоскостью симметрии.

3. Центр симметрии (инверсии). Если тело совмещается с самим собой при инверсии относительно некоторой точки, то эта точка называется центром симметрии или центром инверсии.

Комбинации этих основных элементов симметрии приводит к сложным элементам симметрии, например, к инверсионному повороту, т. е. комбинации поворота с одновременной инверсией и т.п.

При преобразовании рассмотренных выше элементов симметрии хотя бы одна точка остается неподвижной. Поэтому они называются точечными элементами симметрии. В твердых телах и геометрических фигурах возможны оси симметрии любых порядков, в кристаллах же возможны только оси симметрии 1, 2, 3, 4, 6. В них невозможны оси симметрии 5-ого и порядка выше 6-ого. Это ограничение обусловлено тем, что кристаллическое вещество – бесконечная система материальных частиц, симметрично повторяющихся в пространстве. Такие симметричные бесконечные ряды, сетки, решетки, непрерывно заполняющие пространство, несовместимы с осями 5, 7, и других более высоких порядков.

Cингонии.

По характеру симметрии кристалла и его пространственной решетки, от которой зависят, в частности, соотношения между параметрами элементарной ячейки, все виды пространственных решеток могут быть отнесены к одной из семи систем или сингоний (триклинной, моноклинной, ромбической, ромбоэдрической, гексагональной, тетрагональной, кубической).

Характерные особенности каждой сингонии и формулы, связывающие величины межплоскостных расстояний с индексами соответствующих семейств плоскостей и параметрами решетки, т.н. квадратичные формы, приведены в табл.№1.

Пространственные решетки, в которых атомы расположены только в вершинах элементарных ячеек (узлах), называются простыми или примитивными. Решетки, в которых атомы расположены не только по вершинам, но и внутри ячеек и на их гранях, называются сложными.

Очевидно, химические соединения не могут иметь простые решетки. Среди химических элементов простую (ромбоэдрическую) решетку имеет одна лишь ртуть. Для металлов характерны сложные плотно упакованные решетки. Наиболее распространены среди металлов решетки объемноцентрированная кубическая (ОЦК), гранецентрированная кубическая (ГЦК) и компактная гексагональная. Помимо атомов в вершинах (узлах), ячейки этих решеток содержат по одному атому: ОЦК – в центре куба, ГЦК – в центрах каждой из шести граней куба, гексагональная компактная – в центре двух трехгранных призм, образующих параллелепипед.

В простой пространственной решетке на долю одной элементарной ячейки приходится всего один атом (каждой из восьми атомов, расположенных в вершинах, принадлежит одновременно восьми соседним ячейкам 8 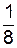=1).

В cложных пространственных решетках на долю элементарной ячейки приходится несколько атомов. Сложные решетки можно рассматривать как совокупность нескольких простых решеток, вставленных друг в друга. Число этих простых решеток равно числу атомов, приходящихся на долю сложной элементарной ячейки.

Сложные решетки называются иногда решетками с базисом. Под базисом решетки понимают совокупность координат атомов, входящих в сложную элементарную ячейку, выраженных в осевых единицах.

В таблице № 2 приведены данные о базисе основных решеток, коэффициенте заполнения 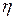(отношения объема, занимаемого атомами, к объему элементарной ячейки) и координационном числе – к.ч. (число ближайших соседних атомов в решетке).

(110). В кубической сингонии их называют плоскостями ромбического додекаэдра.

Плоскости, пересекающие одну ось и параллельные двум другим (например, осям Y и Z) обозначают (100) и называют в кубической решетке плоскостями куба.

Индексы направлений. Под кристаллографическими индексами направления понимают три целых взаимно простых числа, пропорциональных координатам любого атома, лежащего на данном направлении, измеренным в осевых единицах.

При установлении кристаллографических индексов данного направления его необходимо перенести параллельно самому себе в начало координат.

Для кубической сингонии индексы направления 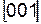, перпендикулярного к плоскостям (001), численно равны индексам этой плоскости. Так индексы оси X равны 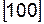, а индексы плоскости, перпендикулярной оси Y, равны (010).

Угол между двумя направлениями в кубической сингонии с индексам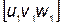и и 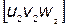может быть найден из уравнения

 

cosj = 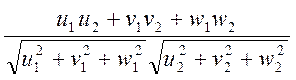(1.5)

 

Совокупность семейств плоскостей, параллельных одному направлению 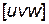в решетке, называется кристаллографической зоной, а само направление осью зоны.

Между индексами оси зоны 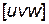и индексами (hkl) плоскостей, входящих в данную зону, имеет место следующая зависимость

 

hu+kv +lv =0 (6)

Уравнение (6) определяет таким образом условие зональности.

Каждое семейство плоскостей с индексами (hkl) характеризуется также своим межплоскостным расстоянием d, то есть расстоянием между двумя соседними параллельными плоскостями

В случае сложной решетки, состоящей как бы из нескольких простых, межплоскостное расстояние равно расстоянию между соседними параллельными плоскостями одной простой решетки. Так в случае ОЦК межплоскостное расстояние для плоскостей (100) равно периоду решетки а, но не а/2.

Между индексами (hkl), величиной d и периодами решетки а,b,c, существует зависимость, различная для каждой сингонии. Приводим в приложении те из них, которые часто используются в рентгеноструктурном анализе поликристаллов.

Все кристаллографически идентичные семейства плоскостей образуют совокупность плоскостей, обозначаемую фигурными скобками {hkl}.Так в кубической сингонии совокупность плоскостей куба {100} содержит шесть кристаллографически идентичных семейств плоскостей 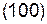, , 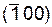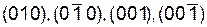. Если, например, путем различных операций симметрии повернуть (001) в любое из остальных четырех семейств плоскостей, то новое положение решетки совпадет с начальным. В этом и заключается кристаллографическая идентичность.

Важнейшим признаком кристаллографически идентичных плоскостей является то, что они обладают одинаковым межплоскостным расстоянием. Поэтому количество кристаллографически идентичных плоскостей (семейств плоскостей) для любой совокупности равно числу возможных перестановок местами и знаками индексов, входящих в данную совокупность, не изменяющих величины межплоскостного расстояния.

В качестве примера рассмотрим те же шесть плоскостей. В случаи кубической сингонии согласно (7) для всех шести семейств плоскостей куба d=a,и они входят в одну совокупность.

В случае тетрагональной сингонии (см. формулу (8)) эти шесть плоскостей разбиваются на две совокупности. В одну из них {100} входят четыре плоскости: (100), 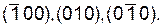Для них d=a.

Во вторую совокупность {001} входят две плоскости (001) и 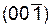. Для них d¹a.

Приводим количество кристаллографически идентичных плоскостей P для совокупностей с разными индексами в кубической сингонии (таблица 4 в Приложении).

В геометрической кристаллографии, изучающей формы кристаллов и многогранников, рассмотренному представлению о совокупности кристаллографически идентичных плоскостей соответствует представление о простой форме. Под простой формой понимают совокупность граней, которые может быть выведена из одной посредством разных операций симметрии.

То же можно сказать и о совокупности кристаллографически идентичных семейств плоскостей. Рассмотрим шлиф поликристаллического образца металла с кубической решеткой, в которой зерна ориентированы беспорядочно. В различных зернах параллельными плоскостями шлифа окажутся разные кристаллографические семейства плоскостей. Если теперь каким либо методом (фигур травления, фигур давления и др.) определить эти плоскости, то окажется (при большом числе зерен), что число зерен, ориентированных параллельно плоскости шлифа плоскостям (100), (110), (111) будет относиться как 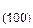P 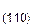: P : P 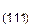=6: 12: 8.

При наличии преимущественной ориентировки (текстуры) это отношение будет нарушено.

Обратная решетка

Для идеального бесконечного монокристалла обратная решетка представляет бесконечное трехмерное распределение точек, расстояние между которыми обратно пропорционально расстояниям между плоскостями прямой решетки. Размерность радиуса-вектора обратной решетки [м-1]. Эта размерность совпадает с размерностью волнового вектора 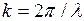. Поэтому множеству радиус-векторов обратной решетки можно сопоставить множество плоских волн. Тогда точное определение обратной решетки можно сформулировать следующим образом:

Множество волновых векторов 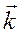образуют обратную решетку по отношению к прямой решетке Бравэ с вектором трансляции 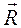, если плоские волны с волновыми векторами 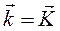имеют периодичность данной решетки Бравэ, т.е.

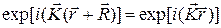или 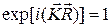(1.7.1)

Обратная решетка всегда определяется по отношению к прямой решетке.

Пусть 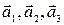- основные векторы прямой решетки, тогда обратную решетку порождают три основных вектора следующим образом:

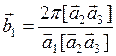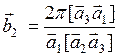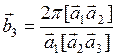, , .(1.7.2)

Докажем, что обратная решетка, построенная на этих векторах также является трансляционной.

Легко показать, что

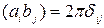, (1.7.3)

,

где 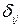- символ Кронекера.

Запишем линейную комбинацию из основных векторов обратной решетки

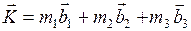, (1.7.4)

где m1, m2 ,m3 - любые числа.

Найдем скалярное произведение векторов 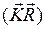. Получим

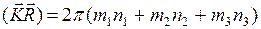(1.7.5)

Если К- вектор обратной решетки, то выполняется равенство

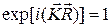, т.е 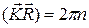, где n целое число. Выражение в скобках в формуле (1.7.5) может быть целым при любых целых n1, n2 ,n3 только если m1, m2 ,m3 также целые числа.

Таким образом, если в выражении (1.7.5) m1, m2 ,m3 - целые числа, вектор 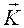является вектором трансляции, а обратная решетка, порожденная этим вектором, также является трансляционной.

Атомная плоскостьрешетки Бравэ – любая плоскость, содержащая, по меньшей мере, 3 , не лежащих на одной прямой, узла.

Семейство атомных плоскостей – множество параллельных, равноотстоящих друг от друга атомных плоскостей, которые в своей совокупности содержат все узлы трехмерной решетки Бравэ. Каждая атомная плоскость является плоскостью какого-либо семейства. Понятие обратная решетка позволяет классифицировать различные семейства атомных плоскостей и очень удобно для структурного анализа.

Такая квалификация основана на теореме, устанавливающей связь между семейством атомных плоскостей и вектором обратной решетки:

для всякого семейства атомных плоскостей, отстоящих друг от друга на расстоянии d, существуют такие векторы обратной решетки, которые перпендикулярны к этим плоскостям, а наименьший из них имеет длину равную 2 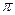/d.

Докажем эту теорему. Пусть имеется семейство атомных плоскостей, отстоящих друг от друга на расстоянии d. Направим плоскую волну: exp[i( 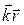)] с волновым вектором k=2 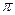/d и единичной амплитудой перпендикулярно данному семейству. Так как это плоская волна, она должна иметь одинаковую фазу на любой плоскости, перпендикулярной направлению распространения волны. Так как плоскости отстоят друг от друга на расстоянии 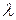, выбранная нами плоская волна будет иметь одинаковое значение фазы на всех атомных плоскостях. Возьмем любой узел на любой атомной плоскости и примем его за начало координат. Тогда 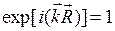и вектор 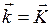, что и требовалось доказать.


Дата добавления: 2021-02-19; просмотров: 499;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.017 сек.