МЕТОДЫ ОЦЕНКИ КАЧЕСТВА РЕГУЛИРОВАНИЯ ЛИНЕЙНЫХ СИСТЕМ

Общие положения

При исследовании систем автоматического регулирования приходится решать задачу обеспечения требуемых показателей качества переходного процесса: быстродействия, колебательности, перерегулирования, характеризующих точность и плавность протекания процесса. Будем, как и в предыдущих главах, предполагать, что система автоматического регулирования описывается системой линейных дифференциальных уравнений с постоянными коэффициентами. При изменении воздействия g(t) на входе системы (рис. 4.1) выходную величину x(t) можно записать

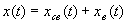, (4.1)

где x(t) — решение дифференциального уравнения, описывающего систему; 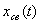— общее решение, соответствующее однородному дифференциальному уравнению. Если последнее не имеет кратных корней, то

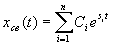, (4.2)

где 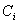— постоянная интегрирования, величину которой определяют параметры системы и начальные условия; 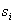— корни характеристического уравнения замкнутой системы D(s) = 0; 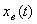— вынужденная составляющая переходного процесса, обусловленная законом изменения g(t).

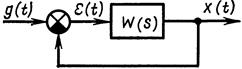
Рис. 4.1

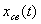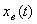Из (4.1) видно, что качество переходного процесса можно оценить по его составляющим и . В этом смысле различают две группы показателей: первая группа — показатели качества переходного процесса 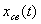; вторая — показатели, характеризующие вынужденную (установившуюся) составляющую 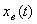, по которой определяют точность системы.

Показатели качества, определяемые непосредственно по кривой переходного процесса, называют прямыми оценками качества. Кривая переходного процесса может быть получена теоретически или экспериментально. Но чаще всего это бывает связано с большими трудностями, так как расчет переходного процесса в системах высокого порядка сложен, а эксперимент не всегда осуществим. Поэтому используют косвенные оценки качества, полученные иным путем, не требующим нахождения кривой переходного процесса. Существующие косвенные методы оценки качества регулирования в линейных непрерывных системах можно разделить на три группы: корневые, интегральные и частотные.