Теоремы А.М. Ляпунова об устойчивости движения по первому приближению
Когда известно общее решение дифференциальных уравнений движения (3.1), можно непосредственно определить значения переменных 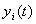 в возмущенном движении, составить вариации
в возмущенном движении, составить вариации 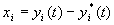 и,
и,  исследуя их, решить вопрос об устойчивости невозмущенного движения
исследуя их, решить вопрос об устойчивости невозмущенного движения 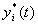 .
.
Однако, как правило, исследование устойчивости движения производят не путем анализа общего решения, а с помощью методов, основанных на качественном анализе дифференциальных уравнений возмущенного движения, которым удовлетворяют отклонения (вариации) 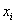 .
.
Чтобы вывести уравнения возмущенного движения, найдем из (3.9) переменные 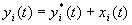 и подставим эти значения
и подставим эти значения 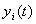 в дифференциальные уравнения движения (3.1). Тогда
в дифференциальные уравнения движения (3.1). Тогда
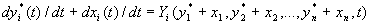 . (3.15)
. (3.15)
Если правые части уравнений (3.15) допускают разложение в ряды Тейлора, то после этого разложения по степеням 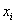 получим
получим
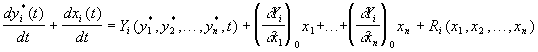 , (3.16)
, (3.16)
где 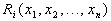 — совокупность членов, зависящих от отклонений
— совокупность членов, зависящих от отклонений 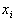 в степени выше первой. Учитывая (3.5), будем иметь
в степени выше первой. Учитывая (3.5), будем иметь
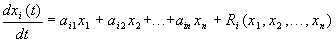 . (3.17)
. (3.17)
В уравнении (3.17) коэффициенты
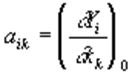 (3.18)
(3.18)
в общем случае являются функциями времени 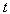 ; в частности, они могут быть постоянными. В дальнейшем, если не будет оговорено особо, будем считать коэффициенты
; в частности, они могут быть постоянными. В дальнейшем, если не будет оговорено особо, будем считать коэффициенты 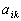 постоянными.
постоянными.
Уравнения (3.17) называют дифференциальными уравнениями возмущенного движения.
Если отклонения 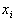 достаточно малы, то, пренебрегая
достаточно малы, то, пренебрегая 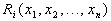 , получим линеаризованные уравнения
, получим линеаризованные уравнения
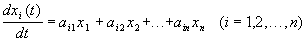 , (3.19)
, (3.19)
называемые уравнениями первого приближения.
Во многих случаях устойчивость движения исследуют по уравнениям первого приближения. Это объясняется не только простотой этого метода, но также и тем, что весьма часто наши знания процессов, происходящих в реальных системах, позволяют надежно определять только первые линейные члены. Однако уравнения первого приближения могут дать иногда совершенно неверное заключение об устойчивости движения. Поэтому, естественно, возникает вопрос об определении условий, при выполнении которых уравнения первого приближения дают правильные ответы об устойчивости движения. Эту исключительно важную и принципиальную для теории автоматического управления задачу впервые поставил и решил А. М. Ляпунов.
Системе уравнений (3.19) соответствует характеристическое уравнение, которое можно записать следующим образом:
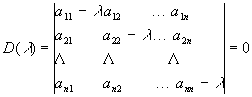 . (3.20)
. (3.20)
Из (3.20) можно найти его корни 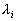 , где i = 1, 2, ...,n, которые в общем случае имеют вид
, где i = 1, 2, ...,n, которые в общем случае имеют вид 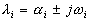 , где
, где 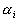 и
и 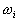 — вещественные и мнимые части корней соответственно.
— вещественные и мнимые части корней соответственно.
Для исследования устойчивости систем по их линеаризованным уравнениям принципиально важны следующие теоремы А. М. Ляпунова, которые приведем без доказательства.
Теорема 1. Если вещественные части всех корней 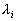 характеристического уравнения {3.20) первого приближения отрицательны, то асимптотически устойчиво.
характеристического уравнения {3.20) первого приближения отрицательны, то асимптотически устойчиво.
Теорема 2. Если среди корней 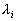 характеристического уравнения {3.20) первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.
характеристического уравнения {3.20) первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.
Если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то этот случай называют критическим. Как показал Ляпунов, в критическом случае устойчивость (неустойчивость) невозмущенного движения не может быть оценена по уравнениям первого приближения, так как она зависит от вида нелинейной функции 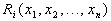 , и поэтому в этом случае требуется рассмотрение дифференциальных уравнений возмущенного движения (3.17) в их исходном виде.
, и поэтому в этом случае требуется рассмотрение дифференциальных уравнений возмущенного движения (3.17) в их исходном виде.
Теоремы Ляпунова имеют важное значение, так как они позволяют судить об устойчивости нелинейных систем по их линеаризованным уравнениям (уравнениям первого приближения).
Дата добавления: 2016-11-29; просмотров: 2627;











