Условия устойчивости линейных систем автоматического управления
Покажем, как на основе изложенного выше определения устойчивости А.М. Ляпунова можно найти условия устойчивости линейных (линеаризованных) систем автоматического управления.
Дифференциальное уравнение линейной системы автоматического управления, записанное для регулируемой выходной величины x(t) при наличии управляющего воздействия g(t), имеет вид:
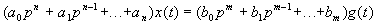 (3.21)
(3.21)
где 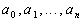 и
и 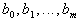 — постоянные коэффициенты, a p — оператор дифференцирования.
— постоянные коэффициенты, a p — оператор дифференцирования.
Изменение регулируемой величины x(t) при произвольном внешнем воздействии g(t) представляет собой решение уравнения (3.21)
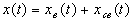 . (3.22)
. (3.22)
В (3.22) первое слагаемое 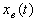 — вынужденная составляющая, имеющая тот же характер, что и правая часть уравнения (3.21). Она определяется как частное решение неоднородного дифференциального уравнения (3.21) с правой частью
— вынужденная составляющая, имеющая тот же характер, что и правая часть уравнения (3.21). Она определяется как частное решение неоднородного дифференциального уравнения (3.21) с правой частью
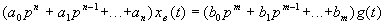 . (3.23)
. (3.23)
Второе слагаемое 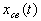 — свободная (переходная) составляющая, которая определяется общим решением однородного дифференциального уравнения (3.21) без правой части
— свободная (переходная) составляющая, которая определяется общим решением однородного дифференциального уравнения (3.21) без правой части
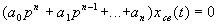 . (3.24)
. (3.24)
Обычно в теории автоматического управления интересуются устойчивостью вынужденной составляющей 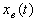 переходного процесса. Поэтому за невозмущенное движение системы необходимо принять вынужденную составляющую переходного процесса
переходного процесса. Поэтому за невозмущенное движение системы необходимо принять вынужденную составляющую переходного процесса 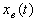 . Тогда возмущенным движением будет любое возможное в системе изменение регулируемой величины x(t), а отклонением или вариацией будет свободная составляющая
. Тогда возмущенным движением будет любое возможное в системе изменение регулируемой величины x(t), а отклонением или вариацией будет свободная составляющая 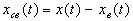 .
.
Возмущениями, по А. М. Ляпунову, являются начальные значения 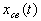 , которые возникли в момент t = to под действием внезапно подействовавших дополнительных внешних сил. Дифференциальными уравнениями возмущенного движения первого приближения в данном случае будут уравнения (3.24). В соответствии с определением устойчивости по А.М. Ляпунову, система будет асимптотически устойчивой, если с течением времени при
, которые возникли в момент t = to под действием внезапно подействовавших дополнительных внешних сил. Дифференциальными уравнениями возмущенного движения первого приближения в данном случае будут уравнения (3.24). В соответствии с определением устойчивости по А.М. Ляпунову, система будет асимптотически устойчивой, если с течением времени при 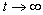 свободная составляющая будет стремиться к нулю, т. е.
свободная составляющая будет стремиться к нулю, т. е. 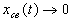 . Чтобы найти эту составляющую, необходимо решить дифференциальное уравнение (3.24).
. Чтобы найти эту составляющую, необходимо решить дифференциальное уравнение (3.24).
Это решение находят как 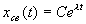 . Дифференцируя это выражение п раз и подставляя в (3.24), после сокращения на общий множитель
. Дифференцируя это выражение п раз и подставляя в (3.24), после сокращения на общий множитель 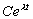 получаем
получаем
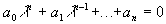 . (3.26)
. (3.26)
Полученное выражение называют характеристическим уравнением. Его корни 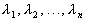 будут определять характер переходного процесса в системе. Нетрудно заметить, что по своему виду левая часть уравнения (3.26) совпадает с дифференциальным оператором при выходной величине в уравнении (3.21), поэтому характеристическое уравнение получают обычно, приравнивая к нулю, дифференциальный оператор при выходной величине в исходном дифференциальном уравнении (3.21), т. е.
будут определять характер переходного процесса в системе. Нетрудно заметить, что по своему виду левая часть уравнения (3.26) совпадает с дифференциальным оператором при выходной величине в уравнении (3.21), поэтому характеристическое уравнение получают обычно, приравнивая к нулю, дифференциальный оператор при выходной величине в исходном дифференциальном уравнении (3.21), т. е.
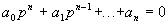 . (3.27)
. (3.27)
Следует заметить, однако, что в характеристическом уравнении (3.27) буква 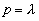 означает уже не символ дифференцирования, а некоторое комплексное число.
означает уже не символ дифференцирования, а некоторое комплексное число.
Решение характеристического уравнения степени п содержит п корней. Корни характеристического уравнения обыкновенного линейного дифференциального уравнения с постоянными коэффициентами могут быть вещественными, комплексными попарно сопряженными, мнимыми попарно сопряженными, нулевыми. В общем случае
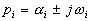 . (3.28)
. (3.28)
Если все корни разные, то их называют простыми. Если среди корней есть одинаковые, то их называют кратными.
Обычно корни с отрицательными вещественными частями принято называть левыми, поскольку они в комплексной плоскости корней расположены слева от мнимой оси, а корни с положительными вещественными частями — правыми корнями.
Условие устойчивости линейной системы формулируется следующим образом: для того чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми.
Вычисление корней весьма просто лишь для характеристических уравнений первого и второго порядков. Поэтому важное значение приобретают правила, которые позволяют определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости.
С помощью критериев можно не только установить, устойчива система или нет, но и выяснить. Как влияют на устойчивость те или иные параметры и структурные изменения в системе.
Критерии устойчивости могут быть разделены на алгебраические и частотные. С математической точки зрения все критерии устойчивости эквивалентны.
Дата добавления: 2016-11-29; просмотров: 2637;











