Оценка качества регулирования в установившемся режиме (коэффициенты ошибок)

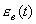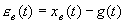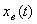Рассмотрим показатели качества, характеризующие вынужденную составляющую ошибки системы. Если на входе системы (рис. 4.1) действует сигнал g(t), то установившаяся ошибка регулирования системы , где — вынужденная составляющая регулируемой величины (4.1).

Если g(t) дифференцируема во всем интервале 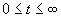, то ошибка системы 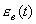может быть представлена в виде ряда

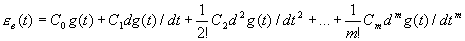, (4.8)

где коэффициенты 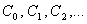принято называть коэффициентами ошибок. Формула (4.8) получена следующим образом. Передаточная функция замкнутой системы относительно ошибки (рис. 4.1)

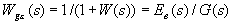. (4.9)

Из (4.9) можно найти выражение для изображения ошибки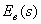

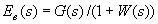(4.10)

Разложим передаточную функцию по ошибке 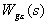в ряд по возрастающим степеням s в окрестности точки s = 0, что соответствует большим значениям времени 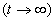, т.е. установившемуся значению ошибки при заданном управляющем воздействии. В соответствии с (4.10) можно записать

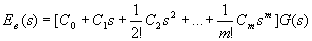. (4.11)

Если передаточная функция 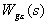является дробно-рациональной функцией

,

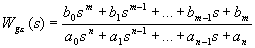то разложение в ряд 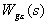можно осуществить делением числителя на знаменатель, располагая члены полинома в порядке возрастания степеней. Переходя в (4.11) от изображений к оригиналам, можно получить для 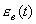выражение (4.8).

Коэффициенты ошибок 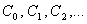определяют по формулам разложения функции 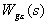в ряд Тейлора

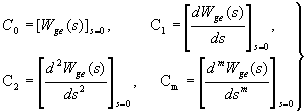(4.12)

Если 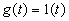, то все производные 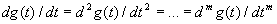=0, и тогд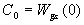а , а .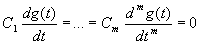

При этом 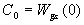— установившееся значение ошибки в замкнутой системе.

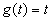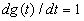Если , то , а 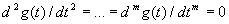; коэффициенты 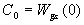), , 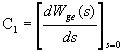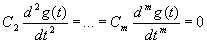и т.д.

Коэффициент 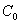принято называть коэффициентом статической или позиционной ошибки; коэффициент 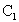— коэффициентом скоростной ошибки; 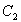— коэффициентом ошибки от ускорения.

В статических системах коэффициент 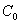отличен от нуля. В системах с астатизмом первого порядка 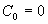, 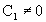. В системах с астатизмом второго порядка 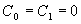, 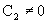. Увеличение числа интегрирующих звеньев в системе приводит к нулевым значениям нескольких коэффициентов ошибок, но при этом усложняется обеспечение устойчивости системы.

Если задающее воздействие имеет ограниченное число производных, отличных от нуля, то ряд (4.8) имеет ограниченное число членов. Метод коэффициентов ошибок применяется при сравнительно медленно меняющихся воздействиях.