Формула взаимосвязи производной по направлению и градиента
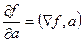 .
.
Доказательство.Обозначим координаты вектора 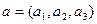 . Точка M произвольная, её координаты
. Точка M произвольная, её координаты 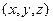 , а точка
, а точка 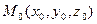 . Так как
. Так как 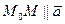 то их координаты пропорциональны, то есть
то их координаты пропорциональны, то есть
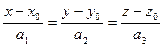 , что также записывается в параметрическом виде:
, что также записывается в параметрическом виде:
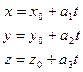
Это функция 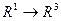 .
.
Рассмотрим производную композиции функций 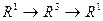 , а именно
, а именно 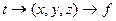 . Одно число (время t) сначала отображается в тройку чисел (координаты точки в момент времени) а затем функция f отображает эти 3 числа снова в одно число.
. Одно число (время t) сначала отображается в тройку чисел (координаты точки в момент времени) а затем функция f отображает эти 3 числа снова в одно число.
Производная внешней функции (которая действует последняя) это вектор-строка градиент функции f.
Производная внутренней функции (которая действует первая) это вектор-столбец.
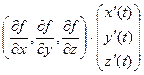
Но ведь 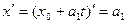 , аналогично
, аналогично 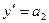 и
и 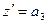 . Тогда
. Тогда
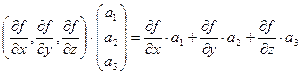
Но это и есть скалярное произведение градиента и вектора 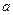 .
.
Отсюда виден смысл градиента.
Геометрический смысл.Градиент это вектор, при движении в направлении которого рост функции наиболее быстрый. Если движение в перпендикулярном направлении, то рост функции будет нулевым. Если под большим увеличением рассмотреть какой-то небольшой кусочек поверхности, то он выглядит почти как наклонная плоскость, а для наклонной плоскости при движении в ту сторону, куда она наклонена, наибольшая скорость роста высоты, в перпендикулярном направлении - высота не изменяется, а при движении в противоположном - уменьшается.
Замечание. Если направление 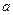 - по координатной оси, то производная по направлению как раз и совпадает с какой-либо из частных производных. Если вектор вдоль оси Ox, то
- по координатной оси, то производная по направлению как раз и совпадает с какой-либо из частных производных. Если вектор вдоль оси Ox, то 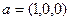 , скалярное произведение этого вектора и градиента
, скалярное произведение этого вектора и градиента 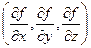 это
это
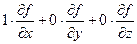 =
= 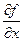 .
.
Дата добавления: 2016-11-29; просмотров: 1711;











