Старшие производные.

После дифференцрования по той или иной переменной, мы получаем снова функцию от тех же нескольких переменных. Но ведь её снова можно продифференцровать по одной или другой переменной. Таким образом, получается n² возможностей определить какие-либо вторые производные, например, если две переменных, то вторых производных будет четыре: , , , .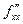

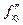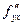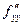Покажем их нахождение в виже схемы:

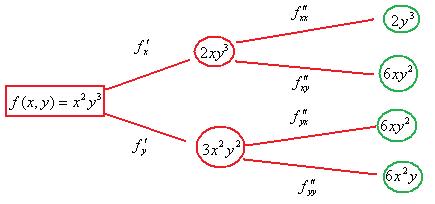
Кстати, смешанные вторые производные 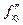, 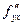всегда совпадают.

Также применяются и такие обозначения:

, , , .

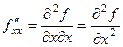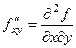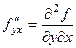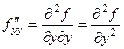Из 2-х производных можно образовать матрицу:

.

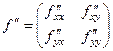Здесь также можно найти 8 третьих производных, 16 четвёртых и т.д.

Кстати, часть из них может быть и 0, так, .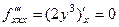

Это был пример с 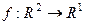. А если 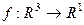, то градиент из 3 координат, тогда есть 9 вторых смешанных частных производных.

Производная функции .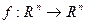

Пусть дано n функций, каждая из них от n переменных:

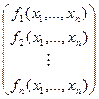
тогда возникает n² возможностей вычислить различные частные производные. Их можно записать в виде матрицы. В случае векторной функции векторного аргумента уже даже первые производные образуют матрицу.

.

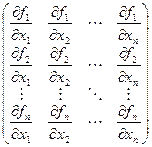Эта матрица и называется производной матрицей функции f.

В каждой из её строк расположен градиент какой-либо из координатных функций .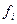

Пример. Найти производную матрицу для функции .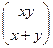

Решение. = = .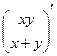

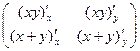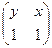Композиция 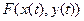и формула полной производной

Пусть задана композиция типа 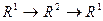, а именно .

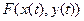Фактически, эта функция является функцией от t (если выразить переменные x,y через t). Следовательно, можно вычислить производную по t. Посмотрим, как эта производная взаимосвязана с частными производными. По правилу дифференцирования композиции,

=

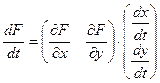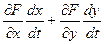
что в других обозначениях можно записать так: .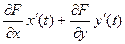

Аналоличная формула верна и в случае 3 координат.