Частные производные и градиент.
Мы рассмотрели случай 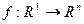 . Как видим, там метод дифференцирования практически ничем не отличается от случая скалярных функций, просто есть n компонент. А теперь рассмотрим производные для функций нескольких переменных
. Как видим, там метод дифференцирования практически ничем не отличается от случая скалярных функций, просто есть n компонент. А теперь рассмотрим производные для функций нескольких переменных 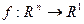 . Пусть например, дана функция
. Пусть например, дана функция 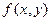 , или
, или 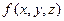 . Приращение аргумента в этом случае задаётся не однозначным образом: ведь можно задать приращение каждому из аргументов, которых несколько. Так, например, для
. Приращение аргумента в этом случае задаётся не однозначным образом: ведь можно задать приращение каждому из аргументов, которых несколько. Так, например, для 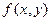 можно фиксировать y и рассмотреть функцию
можно фиксировать y и рассмотреть функцию 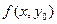 . Это уже будет функция одной переменной. График функции
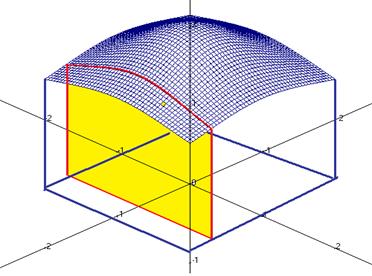
. Это уже будет функция одной переменной. График функции 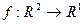 это поверхность, тогда при фиксировании
это поверхность, тогда при фиксировании 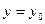 получается сечение поверхности вертикальной плоскостью, то есть кривая.
получается сечение поверхности вертикальной плоскостью, то есть кривая.
Можно задать приращение только для 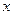 , и тогда получим такое понятие, как частная производная.
, и тогда получим такое понятие, как частная производная.
Определение. Производной функции f по переменной x называется предел:
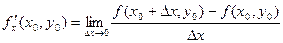 .
.
Кроме 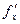 ещё применяют такое обозначение:
ещё применяют такое обозначение: 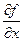 .
.
Аналогично определяется частная производная по y, ведь можно взять вторую точку, отступив в направлении другой оси.
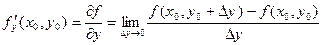 .
.
Геометрический смысл: тангенс угла наклона касательной к кривой, получающейся в одном из сечений.
Физический смысл. Если функция - это температура воздуха, то например, при движении самолёта строго на юг температура за бортом будет возрастать, а при движении на запад или восток почти неизменна. Как видим, частные производные в двух перпендикулярных направлениях могут сильно отличаться.
Дата добавления: 2016-11-29; просмотров: 2354;











