Понятие о задачах оптимизации

Пусть имеются функции 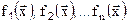, заданные на множестве векторов . Кроме того на этом же множестве векторов определена функция цели .

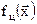Рассмотрим следующую задачу:

,

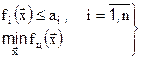которая формулируется следующим образом: найти вектор 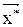такой, что он доставляет минимум функции цели и удовлетворяет ограничениям, наложенным на функции . Решением таких задач занимается теория нелинейного программирования или теория оптимизации. Если функции 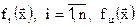являются линейными относительно координат вектора , то задача (7.1) называется задачей линейного программирования, имеет единственное решение, которое находится так называемым симплекс-методом. Если функции 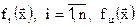являются выпуклыми, то задача (7.1) называется задачей выпуклого программирования, имеет единственное решение, алгоритмы поиска которого хорошо разработаны. В общем случае задача (7.1) имеет множество локальных минимумов и все существующие методы ее решения обеспечивают лишь отыскание вектора 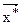, доставляющего лишь один из локальных минимумов функции цели .

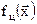Все эти методы основаны на движении от точки (вектора) начального приближения 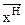к ближайшему вектору решения 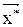, доставляющему локальный минимум. Так как значение функции цели в точке решения 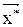меньше чем в точке начального приближения 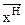, то говорят, что произошла оптимизация начального приближения.

Методы движения делятся на методы нулевого порядка, методы первого порядка, метода второго порядка и т.д. Методы нулевого порядка используют для своей реализации только значения функции. Методы более высокого порядка, кроме значений функции, используют значения производных первого и более высоких порядков. Методы нулевого порядка наиболее просты в реализации, но требуют много времени для поиска решения. Методы более высокого порядка намного эффективнее по скорости поиска решения, но вычисление производных бывает затруднительным, а иногда и невозможным.

Методы нулевого порядка основаны на алгоритме Гаусса-Зейделя или движении по координатам, суть которого состоит в поочередном и пошаговом изменении координат вектора в сторону уменьшения функции цели. Существуют различные модификации метода Гаусса-Зейделя, основанные на преобразовании системы координат в процессе поиска решения.

Один из таких методов нулевого порядка реализован в системе MicroCap 7. Рассмотрим, как можно использовать методы оптимизации в задачах проектирования РЭС.

Как показано в разделе 3.1 проектирование РЭС производится по ТЗ, в котором определены параметры РЭС f₁, … f_n и их граничные значения. Пусть по результатам расчетов требования к параметрам РЭС не удовлетворяются. Выберем из всех компонентов РЭС те из них, которые будем использовать в задаче оптимизации. Образуем из этих компонент вектор , который назовем вектором настройки. Тогда задача улучшения параметров РЭС состоит в нахождении вектора настройки 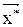, обеспечивающего выполнение неравенств

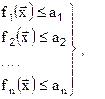(7.2)

где a₁,… a_n – ограничения, наложенные на параметры РЭС в соответствии с требованиями ТЗ.

Разделим и умножим величины, стоящие в правой части неравенств, начиная со второго, на значение a₁:

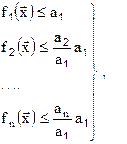(7.3)

Проделаем преобразование (7.3):

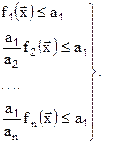(7.4)

Введем новую переменную ε и рассмотрим следующую задачу оптимизации:

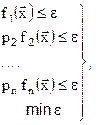(7.5)

где p₂=a₁/a₂,…p_n=a₁/a_n - весовые коэффициенты, устанав-ливающие вес, т.е. важность каждого из ограничений в задаче (7.2).

Пусть по результатам решения задачи оптимизации найден вектор 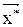и величина ε* = aa_1, где a≤1. Подставляя эти решения в (7.5), убеждаемся, что неравенства (7.2.) выполняются и задача улучшения параметров решена. Если в результате решения задачи коэффициент a>1, то неравенства (7.2.) не выполняются и, следовательно, улучшить параметры не удалось.

Продемонстрируем постановку задачи и порядок оптимизации на примере активного полосового фильтра, синтез которого проведен в разделах 6.2, 6.3. Реализация схемы фильтра с реальными компонентами (рис. 6.9) привела к тому, что оказались не выполнимыми требования к параметрам фильтра в полосе пропускания (рис. 6.10). Как следует из требований (раздел 6.1) параметрами фильтра являются неравномерность усиления Ripple в полосе пропускания [9 кГц, 11 кГц] и разность А усиления в полосах задерживания и пропускания. В качестве компонентов настройки выбираем резисторы R4 и R10, которые образуют вектор =(R4, R10). Параметры фильтра должны удовлетворять следующим условиям:

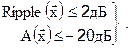(7.6)

В разделе 5.7 представлен набор имеющихся в МС 7 параметров, которые вычисляются по результатам анализа АС. Параметру Ripple соответствует YRange- диапазон изменения модуля коэффициента передачи в полосе пропускания. Параметру А соответствует разность усиления в дБ на частоте 13 кГц и частоте 10 кГц.

В терминах параметров, принятых в МС 7, задача оптимизации записывается в виде

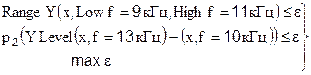(7.7)

В (7.7) весовой коэффициент р=2/20=0,1. Значение весового коэффициента может варьироваться для получения наилучшего решения. Во втором неравенстве записана разность усиления на крайней частоте полосы задерживания 13 кГц и средней частоте полосы пропускания 10 кГц. При этом неравенства для остальных частот полосы задерживания заведомо выполняются.