Порядок проведения статистического анализа

В результате проведения схемотехнического моделирования по двум основным программам получаются функции y=f(x), где “x” – независимая переменная, а “y” – зависимая. Так в программе Transient получается зависимость выходного сигнала U(t) от времени. Поэтому здесь независимая переменная “x” – это время t,а зависимая “y” – это U - напряжение (или ток).

В программе АС получаются зависимости модуля коэффициента передачи |K(f)| от частоты, фазового угла f(t) от частоты и т.д. Здесь независимая переменная х – это частота f, а зависимая у – это f(t), |K(f)| и т.д.

В тоже время режим Монте-Карло имеет дело не с функциональными зависимостями, а с одним параметром, для которого строится гистограмма распределения, рассмотренная в разделе 3.4.

В разделе 3.1 отмечалось, что параметры, указываемые в техническом задании (ТЗ) или в технических условиях (ТУ) на РЭС, представляют собой величины, на которые накладываются лево, право и двусторонние ограничения.

Большинство параметров ТЗ или ТУ могут быть получены из частотных и временных характеристик. Например, пусть имеется характеристика |K(f)|, для fЄ[f₁, f₂]. На этой характеристике имеется максимальное K_max и минимальное K_min значения в диапазоне частот [f₁, f₂]. Разность Δ = K_max – K_min называется неравномерностью АЧХ. Неравномерность АЧХ получена из частотной характеристики и является одним из важнейших параметров фильтровых устройств.

В качестве другого примера рассмотрим переходную характеристику РЭС, т.е. зависимость выходного напряжения H(t) от времени при подаче на вход РЭС скачка напряжения.

Найдем момент времени t₂, при котором выходное напряжение H(t) для t ≥ t₂ отличается от установившегося значения не более, чем на 10%. Найдем, кроме того, начальный момент времени t₁, при котором выходное напряжение H(t₁) составляет десятую часть от установившегося значения. Разница Δt = t₂ – t₁, называется временем установления. Время установления является важнейшим параметром систем автоматического регулирования.

В системе МС7 имеется встроенный набор параметров, которые автоматически вычисляются по результатам анализа АС и Transient.

Они являются теми параметрами, статистические характеристики которых вычисляются в режиме Монте-Карло. Ниже приводятся определения этих параметров, которые иллюстрируются на рис. 5.30.

Rise Time – время нарастания для возрастающей функции между ее заданными минимальным f₁, и максимальным f₂ значениями (рис.5.30,а).

Fall Time – время убывания для убывающей функции между ее заданным максимальным f₂ и минимальным f₁ значениями (рис.5.30,а).

Peak X – точка локального максимума, т.е. значение аргумента Х, при котором функция f(x) достигает одного из локальных максимумов (рис.5.30,б).

Peak Y – один из локальных максимумов, т.е. значение функции f(х) в точке локального максимума (рис.5.30,б).

Valley X – точка локального минимума, т.е. значение аргумента Х, при котором f(x) достигает одного из локальных минимумов (рис.5.31,б).

Valley Y – один из локальных минимумов, т.е. значение функции f(x) в точке локального минимума.

Peak Valley – разность между локальным максимумом и локальным минимумом.

Period – период функции, т.е. разность двух соседних аргументов функции f(x), при которых сама функция достигает среднего значения и далее начинает возрастать. Для исключения начального времени установления период вычисляется при условии, что текущее время больше определенного значения, например, t > 500 нс. С этой целью вводится Булевская переменная β, которая принимает значение false, если условие не выполняется и значение true в противном случае. Таким образом, измерение периода происходит при β=true (рис.5.30,в).

Frequency – частота периодической функции, численно равная величине, обратной периоду.

Width Х – ширина, т.е. разность между двумя ближайшими значениями аргумента Х, при которых функция f(x) принимает заданное значение (рис.5.30,б).

High X – точка глобального максимума, т.е. значение аргумента Х, при котором функция достигает глобального максимума, являющегося наибольшим из всех локальных максимумов (рис.5.30,б).

High Y – глобальный максимум, т.е. значение функции f(x) в точке глобального максимума (рис.5.30,б).

Low X – точка глобального минимума, т.е. значение аргумента Х, при котором функция достигает глобального минимума, являющегося наименьшим из всех локальных минимумов (рис.5.30,б).

Low Y – глобальный минимум, т.е. значение функции f(x) в точке глобального минимума (рис.5.30,б).

X Level – значение аргумента Х, при котором функция принимает заданное значение Y Level (рис.5.30,г).

Y Level – значение функции Y при заданном значении аргумента X = X Level (рис.5.30,г).

X Delta – разность аргументов Х₁ и Х₂, при которых функция принимает заданные значения f(Х₁)=Y1, f(Х₂)=Y2 (рис.5.30,г).

Y Delta – разность значений функции для двух различных значений аргумента (рис.5.30,г)

X Range – диапазон Х, т.е. разность значений аргументов, в которых функция принимает значения глобального максимума и глобального минимума (рис.5.30,б).

Y Range – диапазон Y, т.е. разность между значениями глобального максимума и глобального минимума (рис.5.30,б).

Slope – крутизна (производная) функции в заданной точке.

Phase Margin – запас по фазе, т.е. значение фазы, при котором усиление А_дБ принимает заданное значение.

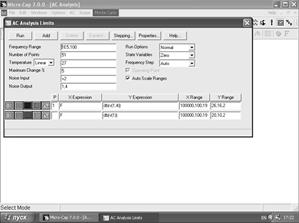
Порядок проведения статистического анализа один и тот же для параметров, заданных в частотной и временной областях. Поэтому проведем статистический анализ АС, выбирая в качестве параметра модуль коэффициента усиления дифференциального усилителя в дБ на частоте 10 кГц. Прежде всего, пользуясь рекомендациями раздела 5.2 (рис.5.13), зададим допуски на все компоненты dev =10 %, при этом изменим имя модели на С6_10%. Переходя к АС анализу (рис.5.20), в окне задания параметров моделирования АС нажмем на кнопку режима Monte Carlo (рис.5.31).

Рис.5.30. Иллюстрация к набору параметров, используемых в МС7

Рис.5.31. Переход к режиму Monte Carlo

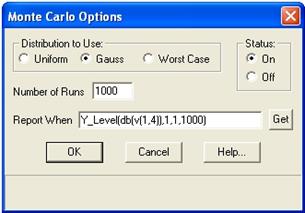
На экране возникает ниспадающее меню, в котором выбирается раздел Options (рис.5.32).

Рис.5.32. Вызов таблицы параметров режима Monte Carlo

Рис.5.33. Таблица параметров режима Monte Carlo

После обращения к этому разделу появляется таблица параметров режима Monte Carlo (рис.5.33).

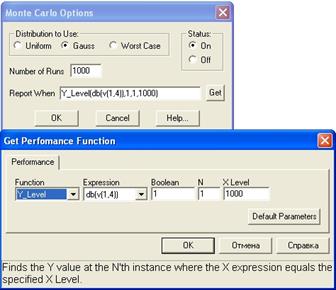
В таблице необходимо выбрать закон распределения (Distribution) случайных параметров компонентов схемы из трех возможных Uniform (равномерный), Gauss (нормальный), Worst Case (наихудший случай). Рекомендуется выбрать закон Gauss. В окне Number of Runs следует указать число испытаний (раздел 3.4). В окне Report When необходимо выбрать вид параметра схемы, для чего следует нажать кнопку Get и перейти в окно выбора параметра схемы (рис.5.35). В этом окне в разделе Function выбирается параметр Y Level, в разделе Expression выбирается параметр db(v(1,4)), так как параметром схемы является значение модуля коэффициента усиления в дБ на частоте 1 кГц. В окно X Level вводится значение частоты 1 кГц.

Рис.5.34. Окно выбора параметра схемы

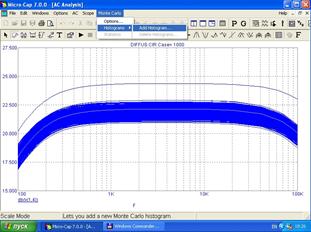
После выхода кнопкой ОК из окна выбора происходит возврат к таблице параметров режима (рис.5.33), где необходимо включить режим Monte Carlo (ON в разделе Status). Далее, перейдя в режим АС, переходим к моделированию (Run). В результате моделирования на экране возникает семейство графиков модуля коэффициента усиления в заданном диапазоне частот. Число графиков равно числу испытаний (рис.5.35).

Рис. 5.35. Семейство графиков статистических испытаний

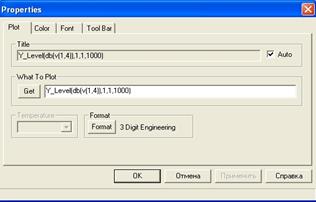
Перейдем теперь к построению гистограммы распределения. Для этого выполняем операцию, представленную на рис.5.36, после выполнения которой появляется таблица оформления гистограммы (рис.5.37).

Рис.5.36. Операция перехода к гистограмме

Рис.5.38. Таблица оформления гистограммы

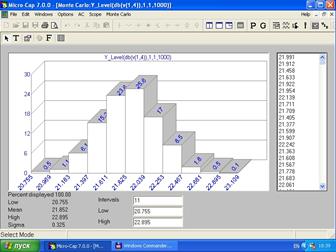
Нажимая ОК, переходим к изображению гистограммы распределения (рис.5.38).

Рис.5.38. Гистограмма распределения

Как следует из гистограммы распределения модуля коэффициента усиления на частоте 1 кГц |К(1кГц)|, его значение лежит в пределах (раздел 3.4):

21,397 дБ ≤ |K(1кГц)| ≤ 22,253 дБ для 81,4% усилителей,

20,88 дБ < |К(1кГц)| ≤ 22,827 дБ для 99,7% усилителей.