Плоские и сферические зеркала

Если перед плоским зеркалом ММ (рис. 12) расположена светящаяся точка С, то лучи СА, СБ, СВ и т. д., идущие из точки С и падающие на зеркало, отразятся от него, образуя углы отражения ОАА', ОББ’, ОВВ’, соответственно равные углам падения САО, СБО и СВО. Проведем из точки С нормаль СНС’ к поверхности ММ и продолжим отраженный луч А'А до пересечения с нормалью.

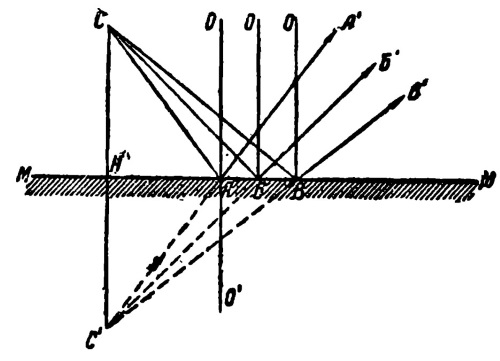
Рис. 12. Отражение в плоском зеркале

В таком случае все лучи будут лежать в одной плоскости-плоскости чертежа. Прямоугольные треугольники САН и С’АН, имея общую сторону НА и равные углы САН и С'АН, равны между собой, так как ОАА' равняется САО по построению, ОАА' = С'АО' по положению, и, следовательно, угол С’ АН = САН. Отсюда С'Н = СН и, следовательно, точка С’ расположена позади поверхности зеркала на таком же расстоянии, на каком точка С находится перед зеркалом.

Так как точку А мы брали произвольно, то все рассуждения могут быть отнесены также к любой точке (Б, В ит. д.). Следовательно, зрителю, находящемуся перед зеркалом, все отраженные лучи будут казаться выходящими из одной общей точки С’, которая называется мнимым изображением точки С в отличие от действительного изображения, которое имело бы место, если бы пересекались сами лучи, а не их продолжения.

Отсюда следует, что для нахождения изображения точки С в плоском зеркале, достаточно провести нормаль к поверхности зеркала и на продолжении этой нормали отложить расстояние НС', равное расстоянию СН точки С от зеркала. Найденная точка С’ и будет мнимым изображением точки С.

Не останавливаясь пока на разнице между действительным и мнимым изображением, заметим, что всякий расходящийся пучок лучей, принадлежащих одной точке тела, мы воспринимаем как изображение этой точки тела, причем самое тело кажется нам расположенным в том месте, откуда пучок кажется исходящим, независимо от того, пересекаются ли действительно эти лучи или пересекаются их продолжения, то-есть является ли данная точка точкой тела, ее действительным или мнимым изображением.

Если вместо зеркала в пучок лучей, идущих из точки С, поместить другую, не зеркальную поверхность, скажем, лист бумаги (рис. 13), который кажется на глаз совершенно гладким, то для лучей света, имеющих длину волны, измеряемую долями микрона, бумага будет представляться сильно шероховатой, как бы бугристой.

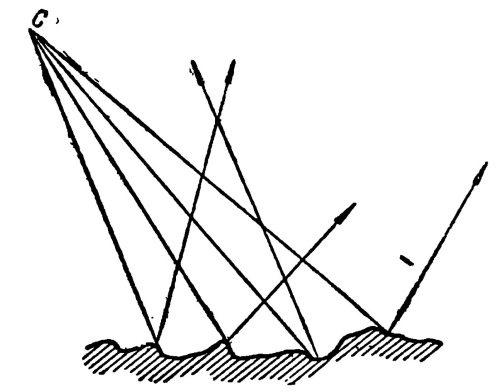
Рис. 13. Отражение от шероховатой поверхности

Хотя в каждом отдельном микроскопическом участке лучи и отражаются по правилу равенства углов, но ввиду того, что отдельные бугры не составляют одной плоскости или правильной поверхности, свет будет рассеиваться по всевозможным направлениям, то-есть будет отражаться диффузно.

В этом случае глаз увидит уже не изображение точки С, а самую поверхность бумаги, тогда как, наблюдая в чистом зеркале изображение светящейся точки, мы не замечаем самой поверхности зеркала. Следовательно, чтобы предмет стал видимым, каждая точка его должна отражать во все стороны лучи, то-есть проявлять те же свойства, какими обладает светящаяся точка.

Таким образом, всякое освещенное тело можно рассматривать как совокупность бесчисленного множества точек, испускающих отраженный свет, подобно тому, как светящаяся точка испускает собственный свет. То же самое мы имеем в случае прохождения света сквозь тело. Поместив между лампой и глазом кусок плоского прозрачного стекла мы свободно различаем лампу со всеми подробностями и не замечаем самого стекла, но если вместо чистого стекла взять стекло матовое, молочное или даже прозрачное, но очень загрязненное, мы хотя и увидим свет, но лампы уже не различаем, зато видим самое стекло. Тут опять мы имеем случай диффузного рассеяния света.

Пусть перед плоским зеркалом (рис. 14) расположена стрелка АБ. Чтобы найти ее изображение в зеркале, достаточно найти изображения крайних точек А и Б. Проведя нормали из точек А и Б и продолжив их за зеркало, откладываем на них отрезки ОА' и НБ', соответственно равные АО и БН, и получаем изображение А'Б' стрелки АБ.

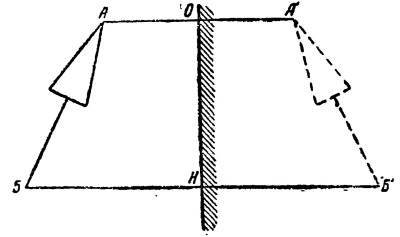
Рис. 14. Построение изображения в плоском зеркале

Следует тут же указать, что нормаль можно проводить не только к поверхности зеркала, но и к ее продолжению. Так, рис. 15 показывает, что глаз, помещенный перед зеркалом ММ, будет видеть изображение А'Б' стрелки АБ, хотя обе нормали, проведенные из концов стрелки АБ, выходят за пределы зеркала.

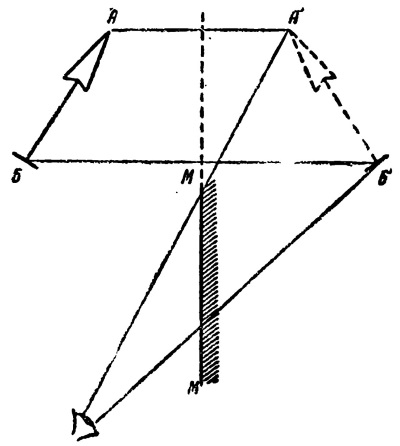
Рис. 15. Видимость изображения в плоском зеркале

В оптических системах встречаются устройства как с одним плоским зеркалом, так и с двумя и несколькими зеркалами. На рис. 16 показана система из двух зеркал ММ и НН, стоящих под углом. Глаз, расположенный перед зеркалом НН, увидит изображение стрелки АБ после двух отражений в виде стрелки А" Б".

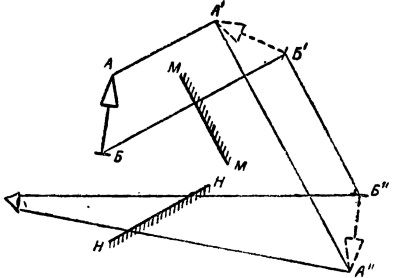
Рис. 16. Изображение в системе плоских зеркал

На рисунке приведена схема построения изображения А'Б’ в зеркале ММ и затем построение в зеркале НН вторичного изображения А‘Б", для которого мнимое изображение А'Б' является предметом. Правила построения здесь те же, что и с одним зеркалом. Чтобы определить пространство, в котором будет видно данное изображение, следует из концов изображения провести прямые через концы плоского зеркала, в котором рассматривается данное изображение.

Если плоское зеркало не закреплено неподвижно, а вращается или качается, поворачиваясь на некоторый угол а, то изображение при этом будет поворачиваться вокруг той же оси на угол, равный 2 α (рис. 17).

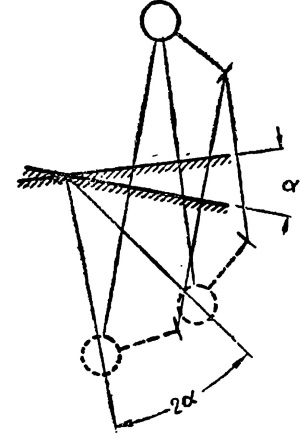
Рис. 17. Изображение в качающемся плоском зеркале

Перейдем от плоского зеркала к сферическому. Если отражающей поверхностью служит внешняя сторона сферы, зеркало будет выпуклым, а если внутренняя полость,— зеркало будет вогнутым.

Возьмем выпуклое зеркало ММ (рис. 18), перед которым расположена стрелка АБ, и проведем из точки А два луча: один AB в произвольном направлении, а другой АО через центр сферической поверхности. Проведем через точку В нормаль ОВР и, построив угол РВГ, равный углу АВР, получим отраженный луч ВГ. В точке А' пересечения продолжений лучей ДА и ВГ будет находиться изображение точки А.

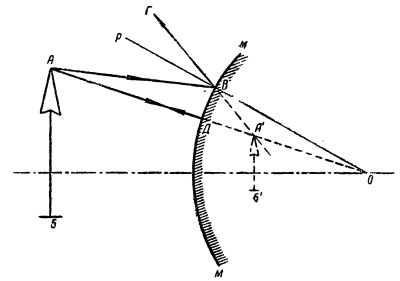
Рис. 18. Изображение в выпуклом зеркале

Точно так же можно построить точку Б', изображающую точку Б. В результате А'Б' будет изображать стрелку АБ.

Как видно из рисунка, изображение будет уменьшенным и прямым. Это изображение—мнимое, так как образовано пересечением не самих лучей, а их продолжений. Выпуклые зеркала имеют относительно небольшое применение. Чаще применяются, особенно в кинотехнике, вогнутые зеркала.

На рис. 19 стрелка АБ находится перед вогнутым зеркалом ММ. Проводим из точки А два луча: один AB — произвольный, а другой АОД —через центр О кривизны зеркала. Проведя через точку В нормаль OB и построив угол ОВГ, равный углу АВО, получим в точке А' пересечения лучей ВГ и ДА действительное изображение точки А. Таким же путем может быть найдено изображение Б' точки Б. Как видно из рисунка, изображение А'Б' — уменьшенное, обратное и действительное.

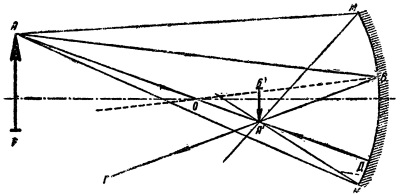
Рис. 19. Уменьшенное изображение в вогнутом зеркале

В отличие от мнимого, действительное изображение можно не только наблюдать глазом, но и воспроизвести на экране. Так, если поместить в плоскости А’ Б’ лист белой бумаги при условии, что стрелка АБ обладает достаточной яркостью, например представляет спираль лампы или окно на фоне неба, на бумаге получится ясно видимое изображение А' Б'.

Проделанные примеры построения изображения показывают, что графическое построение изображения в зеркалах основано на простом использовании закона отражения, то-есть на умении построить отраженный луч, когда дано положение падающего луча.

Нахождение изображения какой-либо точки сводится к нахождению точки пересечения двух лучей, вышедших из одной точки предмета и снова пересекающихся в одной точке после отражения от имеющейся зеркальной поверхности. При этом для облегчения построения берутся не произвольные лучи, а такие лучи, направление которых после отражения заранее известно. Например, луч, падающий по нормали, возвращается по тому же пути в обратном направлении, то-есть отраженный луч совпадает с падающим. В дальнейшем мы увидим, что и в качестве второго луча может быть взят луч, направление отражения которого также заранее известно.

Вернемся к вогнутому зеркалу (см. рис. 19) и представим себе, что каждая точка стрелки АБ излучает неограниченный пучок лучей. В таком случае вся поверхность зеркала ММ будет заполнена этими лучами, и так как любой луч, вышедший из точки А, должен пройти через точку изображения А’, то в точке А' соберутся все лучи, вышедшие из точки А и отраженные от всей поверхности зеркала. Таким образом, вогнутое зеркало превращает падающие на него пучки расходящихся лучей в сходящиеся пучки, то есть собирает расходящиеся пучки. Поэтому вогнутое зеркало часто называют собирательным.

Вогнутое зеркало находит широкое применение в кинотехнике и заслуживает поэтому более детального рассмотрения. Обычно зеркало имеет круглое очертание. Прямая 00', проведенная, через центр кривизны зеркала (рис. 20) и центр окружности, составляемой краем зеркала, называется главной оптической осью зеркала, или просто осью. Точка пересечения оси с поверхностью зеркала называется вершиной зеркала.

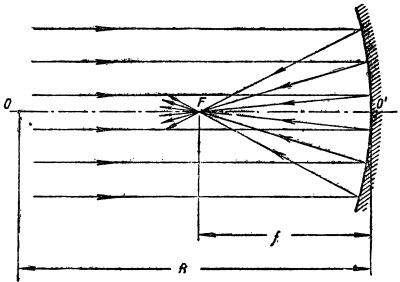
Рис. 20. Положение главного фокуса в вогнутом зеркале

Если на вогнутое зеркало падает пучок лучей, параллельных главной оптической оси, то после отражения лучи пересекаются в одной общей точке F, лежащей на главной оси и называемой главным фокусом зеркала. Расстояние главного фокуса F от вершины зеркала О' называется главным фокусным расстоянием зеркала и обозначается буквой ƒ.

Элементарный расчет показывает, что главный фокус сферического зеркала, если зеркало имеет небольшой диаметр сравнительно с радиусом кривизны, находится от вершины на расстоянии, равном половине радиуса кривизны то-есть:

Всякий луч, падающий на вогнутое зеркало параллельно главной оптической оси, отразившись от зеркала, пройдет через главный фокус, где пересекаются все лучи, идущие к зеркалу параллельно главной оптической оси. Это обстоятельство может быть использовано для построения изображения в вогнутом зеркале, когда известно положение центра кривизны и главного фокуса зеркала.