Уравнение радиолокации

Уравнения радиолокации, используемые для традиционных РЛС, относятся к случаю, когда цель с эффективной площадью рассеяния σ находится на расстоянии R в пределах прямой види­мости от РЛС, имеющей мощность излучения передатчика Р_п, коэффициент усиления передающей антенны G_n и эффективную поверхность приемной антенны A_пр. Указанные уравнения, кото­рые могут быть записаны в различной форме, относятся к надгоризонтной радиолокации. В этих уравнениях учтены потери мощ­ности при распространении радиоволн от передающей антенны до цели и от цели до приемной антенны. Однако в этом случае счи­тают, что распространение радиоволн происходит в пределах пря­мой видимости; отсюда рассматриваемое в уравнениях ослабление мощности при распространении считается обусловленным только сферической расходимостью радиоволн.

В случае загоризонтной радиолокации, когда цель скрыта за пределами горизонта и распространение частично по трассе про­исходит в ионизированном газе ионосферы, потери на трассе име­ют значительно более сложный характер, чем потери за счет сфе­рической расходимости, и обычные уравнения радиолокации ока­зываются непригодными.

Уравнения радиолокации можно представить для отношения мощности принимаемого от цели сигнала Р_пр к мощности шу­ма Р_ш, пересчитанного к входу приемника:

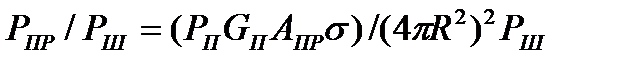(9.1)

Это уравнение относится к простейшему случаю, когда прием и обработка сигналов осуществляются на фоне флуктуационных шу­мов и не учитывается мешающее действие пассивных помех.

Иногда уравнение радиолокации (9.1) для заданных требова­ний на вероятностные характеристики обнаружения, вероятность правильного обнаружения и вероятность ложной тревоги представ­ляют в виде зависимости максимальной дальности обнаружения от энергетических параметров РЛС. Для этого правую часть уравне­ния (9.1) приравнивают некоторому пороговому значению сигна­ла, при котором обеспечиваются заданные вероятностные харак­теристики обнаружения, и из полученного уравнения находят

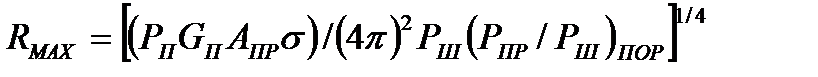(9.2)

Записанное в таком виде уравнение называют уравнением даль­ности радиолокации.

Для надгоризонтной радиолокации распространение радиоволн происходит по прямой, соединяющей радиолокатор и цель; при этом ослабление электромагнитной энергии учитывается множителем W= (4π) ²R⁴ сферической расходимости энергии в прямом и обратном направлениях. Эту величину называют также радиолока­ционным затуханием в свободном пространстве. В отдельных слу­чаях в правую часть уравнения (9.3) вводят дополнительный мно­житель ослабления, который учитывает дополнительные потери на поглощение или рассеяние энергии в атмосфере Земли.

При загоризонтной радиолокации, когда цель скрыта за преде­лами горизонта и распространение происходит в пространстве Земля— ионосфера, затухание радиоволн имеет немонотонный ха­рактер и сложным образом зависит от дальности и высоты цели, характеристик ионосферы и рабочей частоты РЛС.

Рассмотрим основные физические процессы, определяющие мощность принимаемого сигнала цели при загоризонтной радио­локации, ориентируясь главным образом на получение простой интерпретации этих процессов и существенно упрощая при этом их математическое описание.

Пусть в точке 1 (рис. 9.1) на поверхности Земли находится РЛС с антеннами, обеспечивающими направленное излучение. Будем считать, что максимум азимутальной ДН антенны РЛС направлен на цель. Угломестная ДН ориентирована под низкимиуглами,и ее ширина такова, что включает всебя критический угол места γ_кр, выше которого излученная энергия пронизывает ионосферу и теряется в космическом пространстве; при γ<γ_кр излучаемая энергия удерживается ионосферой идалее распространятся в околоземном пространстве. Критический угол места может быть рассчитан в зависимости от параметров ионосферы и рабочей частоты РЛС по формуле

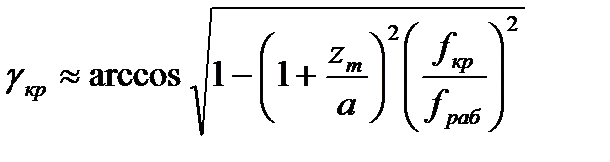
где f_кp — критическаячастота вертикального зондирования ионо- сферы; z_m— высота максимума концентрации слоя F ионосферы; а — радиус Земли.

При выше оговоренных ограничениях можно считать что плотность потока мощности в районе цели, находящейся за горизонтом на расстоянии R и высоте z, будет пропорциональнаP_ПG_П.Такая пропорциональность от G_n может нарушаться, когда критический угол места γ_кр выходит из угломестной ДН антенны РЛС. Плотность потока мощности на дальности R цели с увеличениемG_п при сужении ДН по углу места может при этом даже уменьшаться. Такие условия не являются характерными при нормальной работе РЛС и возникают, когда рабочая частота выбрана неоптимально, т.е. существенно ниже или выше максимально применимой частоты.

Для загоризонтиой радиолокации аналогом урав­нения (9.1) в случае, когда G(γi)=G и А(γi)=А для всех i, j, является формула для отношения сигнал-шум

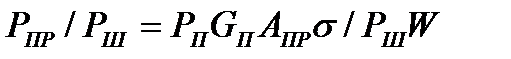(9.3)

Здесь

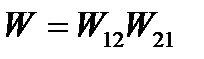(9.4)

Уравнение (9.3) является обобщением известного уравне­ния (9.1) на случаи, когда мощность принимаемого сигнала обус­ловлена суммой мощностей отдельных составляющих, приходящих в точку приема по разным лучам. Подобный случай характерен для загоризонтной радиолокации.

Коэффициент 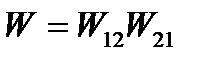, входящий в (9.3), представляет со­бой полное радиолокационное затухание на трассе распростране­ния радиоволн, т.е. затухание в прямом и обратном направлениях. Затухание электромагнитной энергии при распространении радиоволн от РЛС до цели W₁₂ за­висит от дальности R. Аналогичная за­висимость от R будет иметь место и для затухания в обратном направлении W₁₂, т.e. от цели до РЛС. Это определяет и харак-Л тер зависимости от дальности R суммарного радиолокационного ' затухания на трассе W.

K соотношению вида (9.3) можно прийти и из других сообра­жений. Предположим, что РЛС облучает цель, эффективная по­верхность рассеяния которой σ. Тогда мощность отраженного сиг­нала Р_пр на входе приемного устройства РЛС можно представить в виде произведения трех сомножителей:

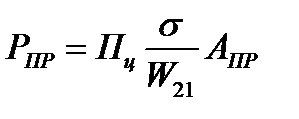. (9.5)

Первый множитель П_Ц определяет плотность потока мощности, облучающей цель; произведение первого множителя на второй 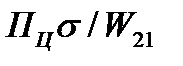— плотность потока мощности отраженной волны в месте расположения приемной антенны. Умножая полученную величину на эффективную поверхность приемной антенны А_пр, находим мощность отраженного сигнала, поступающего на согласованный вход приемника РЛС. Представим (9.5) в развернутом виде:

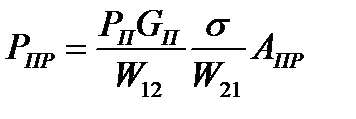
Переходя от мощности на входе приемника Р_пр к отношению сигнал-шум по мощности Р_пр/Р_ш, получаем (9.3). Соотноше­ние (9.3) может быть использовано как для однопозиционной РЛС, так и для двухпозицнонной, в которой передающая и приемная антенны разнесены на некоторое расстояние.

Уравнение (9.3) можно рассматривать как уравнение идеального радиолокатора, в котором все параметры выбраны оптималь­ным образом. В реальной РЛС всегда имеются энергетические потери, связанные с несогласованностью фидерных ВЧ трактов, неоптималыюстью обработки сигналов и другими причинами. Эти энергетические потери можно учесть, вводя в (9.3) коэффициент потерь. При этом (9.3) примет вид

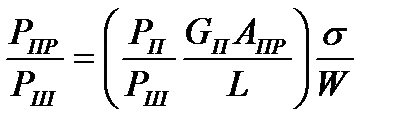, (9.6)

где L — коэффициент потерь.

Преобразуем эту формулу, введя вместо отношения P_пр/P_ш отношение Э_С/N₀, гдеЭ_с- энергия принимаемого сигнала, а N₀=P_Ш/П_Ш(P_Ш — среднеквадратическая мощность шума; N₀ — его спектральная плотность, т. е. мощность шума на единицу шумовойполосы П_ш).

Учитывая, что за время локации цели все величины, входящие в равенство, за исключением Р_п и Р_пр, можно считать по­стоянными, проинтегрируем правую илевую части равенства в пределах длительности облучающего цель сигнала t₃ и отражен­ного от цели принимаемого сигнала t_np, причем примем, что t₃= t_пр= t.Тогда, имея в виду, что

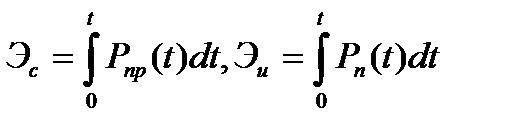. (9.7),(9.8)

Вместо (9.8) получаем

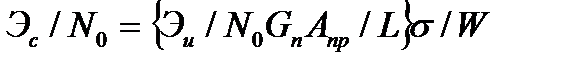, (9.9)

где Э_с иЭ_и— энергиипринимаемого иизлучаемого сигналов со­ответственно.

Формула (9.9) получена для отношения сигнал-шум, особен­ность которого состоит в том, что оно не зависит от формы сигнал-шум,т.е. от вида огибающей и способа внутриимпульсноймоду­ляции.