ВОЗМОЖНОСТИ И ПРИМЕРЫ ПОЛУЧЕНИЯ ДАЛЬНОСТНЫХ ПОРТРЕТОВ

Зависимость качества распознавания объектов с различными алфавитами их классов от разрешающей способности по дальности может быть установлена методом математического моделирования (разд. 4). С общих позиций, желательно повышение разрешающей способности по дальности, однако чрезмерное ее повышение, дробя сигнал, увеличивает пороговую энергию обнаружения. С учетом наличия малоразмерных целей, с одной стороны, и желательности ограничения стоимости - с другой, могут реализовываться разрешающие способности порядка метра - единиц метров для воздушных целей и порядка долей метра для космических и баллистических целей. Для согласованного разрешения потребная полоса частот составляет 150 МГц - доли от 150 МГц в первом случае и более 150 МГц - во втором (см. также разд. 1.5.1).

Сигналы с указанными полосами могут быть широкополосными (частотно-модулированными, фазоманипулированными, частотно-манипулированными), а также многочастотными. Широкое внимание было уделено в предшествующие годы линейно-частотно-модулированному (ЛЧМ) сигналу, для обработки которого не требуется сложная элементная база.

3.2.1. МЕТОДЫ КОГЕРЕНТНОЙ ОБРАБОТКИ СИГНАЛОВ

При когерентной обработке сигналов могут использоваться корреляционный, фильтровой и корреляционно-фильтровой ее методы [43, 113].

Корреляционная обработка, аналоговая в частности, требует большого чис­ла корреляторов, определяемого произведением полосы частот на временной интервал, соответствующий "окну наблюдения" по дальности. Фильтровая об­работка ограничений в "окне наблюдений" по дальности не требует, но обес­печивается изготовлением сложных аналоговых или цифровых фильтров сжа­тия. Усложняются и устройства последетекторной обработки. Корреляционно-фильтровая обработка ЛЧМ-сигнала обеспечивается подачей на первый смеситель приемника в определенный момент времени после излучения зондирующего сигнала гетеродинного ЛЧМ-импульса, полностью или частично демодулирующего принимаемый сигнал по частоте, и последующей фильтрацией.

При частичной демодуляции полоса частот снижается на 1 - 2 порядка, что облегчает построение фильтра сжатия и устройств последетекторной обработки. Можнообеспечить одноканальный прием при размере окна, достаточном для наблюдения дальностных портретов одной-двух целей. В случае числа каналов приема, пропорционального уменьшению полосы частот, можно наблюдать всю дальность, но уже 1-2 канала, работающие по целеуказанию, могут обеспечить высокую пропускную способность,

При полной частотной демодуляции фильтры сжатия и детекторы заменя­ются цифровыми или аналоговыми амплитудными спектроанализаторами.

Ниже приводятся примеры технической реализации высокого разрешения по дальности для ЛЧМ зондирующих сигналов при различных видах обработ­ки (фильтровой, корреляционно-фильтровой с частичной и полной частотной демодуляцией).

3.2.2. ПРИМЕРЫ КОГЕРЕНТНОЙ ОБРАБОТКИ СИГНАЛОВ

Фильтровая обработка ЛЧМ-сигналов использовалась в макетах РЛС с широкополосными ЛЧМ импульсными сигналами в 60-х годах в СССР и в США. Так в [37, 38] описана реализация макета РЛС с фильтром сжатия на кабеле с отводами. Частотная девиация составила Δf = 75 МГц, длитель­ность импульса - 2 мкс, их произведение - 150. В [62] описана реализация макета с волноводным фильтром сжатия. Частотная девиация Δf =150 МГц, длительность импульса τ_и= 1 мкс, их произведение также равно 150.

Корреляционно-фильтровая обработка ЛЧМ-сигналов с частичной частотной демодуляцией, апробированная в СССР в начале 60-х годов [37], реали­зована в начале 70-х годов в экспериментальных РЛС США. РЛС, установ­ленные на острове Флойд [63], работают в режиме поочередного излучения сравнительно узкополосных и более широкополосных радиоимпульсов десяти­сантиметрового диапазона. Для первоначального определения дальности объек­та служат ЛЧМ-импульсы с девиацией частоты Δf =2,5 МГц. Высокое раз­решение по дальности обеспечивается импульсами с девиацией частоты Δf = 250 МГц, длительностью τ_и = 20 мкс, с произведением τ_и Δf= 5000.

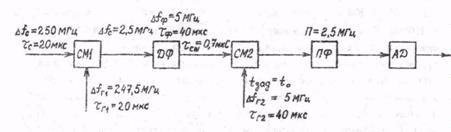
Рис. 3.1. Структурная схема тракта корреляционно-фильтроеой обработки ЛЧМ-сигнола с частичной его частотной демодуляцией.

Обработка принимаемых широкополосных импульсов поясняется схемой (рис. 3.1). К моментам прихода от элементов цели ЛЧМ-импульсов на первый смеситель приемника подается гетеродинный ЛЧМ-импульс с девиацией частоты 250 - 2,5 = 247,5 МГц на протяжении20 мкс. Импульсы промежу­точной частоты от элементов цели имеют, поэтому частотную девиацию 2,5 МГц при их длительности 20 мкс, причем центральные частоты этих импульсов зависят от точных значений дальности. Импульсы промежуточной частоты обрабатываются поэтому в дисперсионном фильтре сжатия с удвоенными час­тотной девиацией 5 МГц и длительностью импульсной характеристики 40 мкс, причем сжатые импульсы имеют по-прежнему неодинаковые центральные частоты. Последние выравниваются во втором смесителе. Для этого на второй его вход с задержкой (20 – t₀) мкс относительно первого гетеродинного им­пульса подается второй с девиацией частоты 5 МГц на длительности 40 мкс; здесь t₀ - минимальная задержка дисперсионного фильтра.Оконечный фильтр сужает полосу пропускания приемника с 5 до 2,5 МГц и позволяет осущест­вить весовую обработку. Общее сужение ширины спектра сигнала в 100 раз примерно с 250 МГц до 2,5 МГц не ухудшает в данном случае разрешающей способности по дальности. Дело в том, что за счет описанных гетеродинно-дисперсионных преобразований одновременно с растяжением длительности сжатого импульса в 100 раз, во столько же раз растягивается и масштаб времени [38, 43]. Издержкой является лишь сокращение "окна наблюдения" до 30 м.

Корреляционно-фильтровая обработка ЛЧМ-сигналов с полной частотной демодуляцией реализована в конце 70-х годов на РЛС 25-сантиметрового диапазона АN/FРS-115 США [64]. Для первоначального определения дальности, других траекторных параметров объекта, выявления при этом признаков распознавания предусмотрено излучение радиоимпульсов с частотными девиа­циями 1 и 5 МГц. После этого могут излучаться импульсы с частотной деви­ацией Δf = 200 МГц длительностью τ_и = 1000 мкс, с произведением τ_и Δf = 200000. К моментам прихода отраженных элементами цели импульсов, оцениваемых по результатам предыдущих зондирований, на первый смеситель приемника подается гетеродинный ЛЧМ-импульс с частотной девиацией 200 МГц на протяжении 1000 мкс. Выходной сигнал смесителя сводится при этом к наложению немодулированных по частоте импульсов, центральные частоты которых определяются различающимися между собой дальностями элементов цели. Суммарный сигнал оцифровывается и подвергается спектральному ана­лизу путем проведения БПФ с размерностью около 16ּ10³. За счет паралле­лизма цифровой обработки данные выдаются в масштабе времени, близком к реальному. Размер окна наблюдения по дальности - около 4 км, растяжение временного масштаба - 40.

3.3. ПРИНЦИПЫ РЕАЛИЗАЦИИ ВЫСОКОГО РАЗРЕШЕНИЯ ЗА СЧЕТ ПРЯМОГО СИНТЕЗА АПЕРТУРЫ

Общие соотношения прямого синтеза апертуры приводятся для локаторов обзора поверхности с летательных аппаратов [25, 41, 65]. Истинная характе­ристика направленности антенны отклонена в общем случае на угол a₀ от линии пути (рис. 3.2).

Обзор при a₀ =90° называют боковым, это наиболее распространенный вид обзора. Обзор при 0°< a₀ <90° называют переднебоковым (рассматривается главным образом в связи с обратным синтезом). Высота полета явно в расчет не вводится. При конечной высоте угол a₀ отсчитывается в плоскости, наклонной по отношению к наблюдаемой поверхности. Пусть длина истинного раскрыва антенны вдоль линии пути равна d.

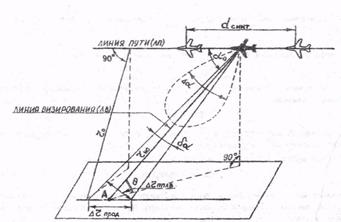
Рис. 3.2. К пояснению принципа прямого синтеза апертуры

С учетом работы антенны на передачу и прием характеристике направленности, формируемой истинным раскрывом, можно приписать эквивалентную ширину в радианах:

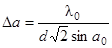.(3.1)

От каждого элемента земной поверхности при импульсном его зондирова­нии принимается пачка отраженных радиоимпульсов. Максимальная длительность пачки

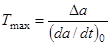, (3.2)

где 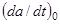- угловая скорость поворота линии визирования в момент прохождения t=0 оси характеристики направленности через элемент А. Ее величина определяется отношением проекции vsin a₀ вектора путевой скорости на плоскость, перпендикулярную линии визирования к наклонной, дальности r_н0 до наблюдаемого элемента в момент времени t=0. Она может быть выражена также через не зависящую от времени дальность этого элемента r₀ = r_н0sin a₀ до линии пути.

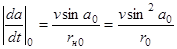. (3.3)

Вследствие изменения дальности r₀ изменяется доплеровская частота

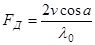
с пропорциональной (3.3) скоростью изменения в момент t =0

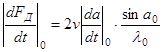(3.4)

За время -Т/2≤ t ≤ Т/2(Т≤ Т_mах) при |Δa|<< 1 имеет место час­тотная девиация

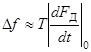(3.5)

Линейной при |Δа|<<1 модуляции частоты пачки импульсов соответст­вует квадратичная модуляция ее фазы bt², b=πΔf / T.

При b(T/2)² ≤ π/4 или, иначе, при

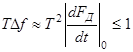(3.6)

обоими взаимосвязанными видами модуляции можно пренебречь. В силу (3.3) - (3.4) это соответствует дальней зоне (зоне Фраунгофера) приемно-передающей антенны с синтезированным раскрывом vТ

,

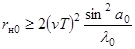которая подобна дальней зоне передающей антенны с обычным раскрывом d. Какой-либо фокусировки по дальности при этом не требуется. По мере же увеличения синтезированного раскрыва объект А попадает во френелевскую зону и фокусировка становится необходимой. Учет связанных с частотной мо­дуляцией квадратичных сдвигов фаз bt² как раз и обеспечивает эту фокусиров­ку.

Мера разрешающей способности вдоль линии пути при сфокуси­рованном раскрыве может быть оценена с позиций временного, частотного и пространственного анализа.

Так, разрешающая способность Δr_прод вдоль линии пути определяется скоростью v носителя РЛС и временной разрешающей способностью Δt =1/Δf ЛЧМ-колебаний после их согласованной фильтрации. Тогда с уче­том приведенной для Δf цепочки соотношений

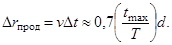(3.7)

Частотный (спектральный) анализ проводится после фазовой коррекции, эквивалентной гетеродинированию принимаемых колебаний с целью снятие (по результатам траекторного анализа) частотной девиации Δf. При разреша­ющей способности по доплеровской частоте δF_д =1/Т обеспечивается угло­вая разрешающей способность да. Из выражения доплеровской частоты следует

.

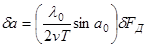С позиций пространственного (антенного) анализа та же величина, δа вводится как ширина характеристики направленности синтезированного раскрыва d_синт = vT после фазовой коррекции

.

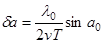Коэффициент 2 (а не 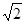) в знаменателе связан с совместным, а не раздельным учетом разностей хода при передаче и приеме.

В двух последних случаях для наклонной дальностиr_н0 обеспечивается мера поперечной по отношениюк линии визирования разрешающей способности Δr_пплв»r_ноdа.С другой стороны, мера Δr_пплв является проекцией меры разрешающей способности вдоль линии пути Δr_пплв = Δr_продsin a₀ . Таким образом, с учетом цепочкиприведенных соотношений

.

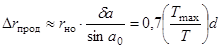Со всех трех позиций рассмотрения приходим, таким образом, к общему выводу. Мера разрешающей способности Δr_прод уменьшается, т. е. разрешающая способность повышается с увеличением времени когерентной обработки Т и размера синтезированного раскрыва vT. В принятых теоретических предположениях наивысшая разрешающая способность вдоль линии пути Δr_прод » 0,7 d достигается при T=T_max . Найденная величина не зависит ни от дальности r₀, ни от углового параметра 1/sin a₀ = cosec a₀. Увеличение последних, существенное при фиксированном раскрыве антенны, компенсируется увеличением синтезированного раскрыва.

Мера (3.7) увеличивается, а разрешение ухудшается с увеличением истинного раскрыва антенны d, поскольку при одноканальном и неследящем приеме это приводит к уменьшению размера синтезированного раскрыва. Примногоканальной (многоэлементной) антенне, например, и накоплении информации каналов с временными сдвигами можно получить меру разрешающей способности, определяемую размерами элементов антенны, а не всей антенной в целом.

Мера разрешающей способности при несфокусированном раскрыве реализуется при далеко не полном использовании синтеза, выборе Т << Т_maxс целью работы в дальней зоне без фокусировки на отдельные участки даль­ности. Максимальное время накопления согласно критерию (3.6)

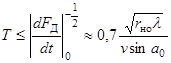
приводит к мере разрешающей способности вдоль линии пути

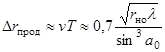(3.8)

С увеличением r_но разрешение ухудшается.

Замечание о числовых коэффициентах в выражениях(3.1), (3.7), (3.8). Поскольку речь идет об ориентировочных мерах разрешающей способности, коэффициенты 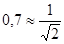явно приближенные. В литературе вместо коэффициентов 0,7 часто приводят коэффициенты 0,5, предваряя их более сложными, чем здесь, выкладками. Однако физические предпосылки этих выкладок типа "равномерное распределение поля на раскрыве" и "уро­вень отсчета по половинной мощности" носят также ориентировочный харак­тер.

Частота следования импульсов. Для воспроизведения спектра доплеровских частот она должна превышать частотную девиацию (3.5)

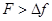(3.9)

Мера разрешающей способности поперек линии пути при боковом обзоре (а₀ =90°). Определяется выражением

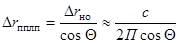, (3.10)

где Dr_но - разрешающая способность вдоль линии визирования (наклонной дальности), П - полоса частот сигнала, Θ - угол между линией наклонной дальности и наблюдаемой поверхностью.

3.4. ПРИМЕР СИНТЕЗА АПЕРТУРЫ НА СПУТНИКЕ "Сисат", США, 1978 [41]

Высота полета - около 800 км, скорость - 6,6 км/с. Размер антенны - 2,2 х 10,7 м². Длина волны 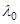= 0,235 м. Обзор боковой a₀ =90°. Луч антенны, расположенный в плоскости нормальной траектории спутника, откло­нен от нормали к поверхности Земли на угол 23°. Полоса частот П = 19 МГц. Время когерентного накопления Т = 0,68 с. Импульсы излучаются с частотами следования 1463, 1537 и 1645 Гц. Некогерентное накопление пол­учаемых на указанных частотах данных снижает роль флюктуаций вторичного излучения элементов разрешения просматриваемой местности. Все эти частоты удовлетворяют условию (3,9) и обеспечивают, кроме того, однозначность из­мерения дальности просматриваемой поверхности Земли в полосе наблюдения 100 км. Меры разрешающей способности поперек и вдоль линии пути опреде­ляются соотношениями (3.7) и (3.10). Реальную разрешающую способность оценивают величиной квадрата со сторонами 25 х 25 м². Время накопления Т < Т_мах и длина синтезированного раскрыва vT= 6,6·0,68= 4,5 км несколько менее потенциально возможных. Поэтому и расчетная мера разрешающей способности вдоль линии пути примерно втрое превышает потенциально воз­можную, определенную по формуле (3.7):

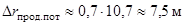
3.5. ОБРАТНЫЙ (ИНВЕРСНЫЙ) СИНТЕЗ АПЕРТУРЫ

И ФОРМИРОВАНИЕ ДАЛЬНОСТНО-УГЛОВЫХ ПОРТРЕТОВ

Может проводиться в режимах слежения РЛС за выделенными целями. Как и в случае прямого синтеза, могут формироваться сфокусированные и несфокусированные синтезированные раскрывы [40, 41, 66].

Возможны, по-прежнему, пространственная, частотная и временная трак­товки повышенного углового разрешения. Поворот а линии визирования от­носительно оси характеристики направленности антенны локатора заменяется поворотом а вектора скорости цели относительно линии визирования, в обоих случаях за конечное время -Т/2≤ t ≤ Т/2. Согласованная угловая разрешающая способность синтезированного раскрыва равна, как и ранее,

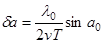
От нее переходят к линейной разрешающей способности. Однако вместо разрешающей способности вдоль линии пути Δr_прод вводится линейная разре­шающая способность в плоскости, поперечной линии визирования,

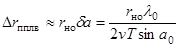(3.11)

где r_но - по-прежнему наклонная дальность.

Поскольку 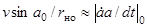– это скорость поворота цели относительно линии визирования, то произведение ее на время Тдает соответствующее изменение Dа(Т) угла а. Следовательно, справедливо также соотношение

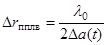(3.12)

Для осуществления фокусировки изображения поступательно движущейся цели возможны различные методы (см. также разд. 3.6).

Возможно, в частности, адаптивное фазирование по типу метода внешней когерентности. Пусть, например, из разрешаемых по дальности элементов це­ли алгоритмически выделяется некий доминирующий элемент [40], удовлетво­ряющий требованиям достаточной интенсивности отраженного сигнала и устойчивости амплитуды на протяжении пачки импульсов. Частотно-фазовая моду­ляция сигнала от этого элемента используется для демодуляции сигналов от остальных элементов. Разрешение в плоскости, поперечной линии визирования, обеспечивается после этого путем спектрального анализа, как и при пря­мом синтезе. При широких полосах П существенно, однако, предварительное выравнивание временных запаздываний дальностных портретов, устанавли­ваемое по максимуму их корреляции.

При использовании единственного опорного напряжения существуют опре­деленные, хотя и не всегда существенные ограничения на размеры цели. Пусть d(Df) - изменение введенной выше частотной девиации, связанное с изменением наклонной дальности r_н0 на δr_н0. Для просмотра радиального интервала ± δr_н0 с использованием единственного опорного напряжения по аналогии с (3.6) (см. также (3.3), (3,4)), необходимо, чтобы

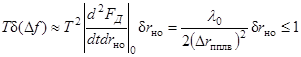, (3.13)

где по-прежнему, 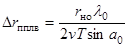– разрешающая способность попе­рек линии визирования.

Можно показать [41], что аналогичные ограничения накладываются и на размер цели, поперечный линии визирования.

При Δr_пплв=2 м и длинах волн λ₀ =0,1м и λ₀ = 0,03м радиусы чет­кости изображения вдоль линии визирования (δr_н0 )_max в частности, равны 80 м и 267 м соответственно.

Особенности инверсного синтеза апертуры при чисто вращатель­ном движении цели. Движение цели рассматривалось до сих пор только как равномерное поступательное. Полученные соотношения, тем не менее, по­казала, что при условии фазовой коррекции (фокусировки) разрешающая способность поперек линии визирования Δr_пплв определяется только малым углом ее поворота за время наблюдения относительно линии визирования Δа и длинной волны λ₀. То же самое имеет место, если цель совершает равномер­ное вращательное движение вокруг собственной оси без элементов поступа­тельного движения. В плоскости, нормальной оси вращения, Δr_пплв= λ₀ /2Δа, в чем можно убедиться как со спектральных (частотных), так и с антенных (пространственных) позиций.

Со спектральных позиций существенно, что отражатели, расположенные в плоскости поперечной линии визирования, имеют различные радиальные ско­рости в зависимости от расстояния до оси вращения. Разрешение поперек ли­нии визирования сводится к разрешению по доплеровской частоте.

С антенных позиций вращение цели относительно неподвижного локатора заменяется вращением локатора относительно цели.

Несмотря на вращательный характер движения, замена оказывается допу­стимой, поскольку эффекты инерции не принимаются во внимание. Синтезируемая же апертура сводится к малому участку цилиндра. Расстояние "лока­тор – цель" на ней не меняется, частотной модуляции сигнала не происходит, фазовой коррекции не требуется.

Вращение макетов целей в сочетании с обработкой, обеспечивающей син­тез апертуры, используется в последнее время для выявления вкладов отдель­ных элементов цели в суммарные эффекты их вторичного излучения.

Собственные вращения реальных целей могут накладываться на их поступательное движение. Учет возникающих при этом эффектов в процессе обрат­ного синтеза апертуры требует специального рассмотрения.

3.6. ВАРИАНТЫ АДАПТАЦИИ К СЛУЧАЙНЫМ ПАРАМЕТРАМ СИГНАЛОВ

Движение реальных аэродинамических целей характеризуется более слож­ными, чем отмечалось в разд. 3.5, закономерностями. Так, даже в случае, когда пилот пытается выполнить полет с неизменным курсом и постоянной скоростью, точка центра масс самолета движется в пространстве с непостоян­ной скоростью. Кроме того, движение аэродинамической цели характеризуется случайными рысканиями по углам курса, крена и тангажа. Указанные явления обусловлены турбулентностью атмосферы.

Непостоянство скорости движения точки центра масс самолета, движущею­ся с постоянными углами сноса и скольжения, приводит к возникновению случайных набегов фаз на синтезируемой апертуре. Наличие же рысканий приводит к тому, что величина и направление вектора угловой скорости вращения цели относительно наземного радиолокатора становятся случайными. Это, в свою очередь, вызывает появление случайной составляющей амплитудно-фазового распределения на синтезируемой апертуре. Оба указанных явления приводят к расфокусированию апертуры и, в конечном итоге, к разрушению дальностно-азимутального портрета цели.

Наиболее существенный вклад в расфокусирование апертуры вносит нерав­номерность движения по радиальной дальности точки центра масс самолета. Расфокусирование апертуры по этой причине может произойти за время в несколько десятков миллисекунд. Наличие угловых рысканий цели приводит к разрушению когерентности эхо-сигнала и расфокусированию апертуры на ин­тервале времени более 0,3...1 с [40].

Рассмотрим варианты адаптации к случайным параметрам эхо-сигналов при получении радиоизображений аэродинамических целей. Излагаемый материал иллюстрируется двумерными изображениями, получаемыми при модели­ровании

3.7. АДАПТАЦИЯ К НЕРАВНОМЕРНОМУ ДВИЖЕНИЮ ЦЕЛИ БЕЗ УГЛОВЫХ РЫСКАНИЙ

Алгоритмическое совмещение огибающих дальностных портретов и введе­ние опорного элемента (разд. 3.5) решает задачи не только фокусировки изо­бражения, но и учета неравномерности движения цели без угловых рысканий. Одновременно учитываются нестабильности передающего устройства, гетеродина и т.д. Опорный элемент выделяется по минимуму дисперсии амплитудных флюктуаций сигнала. Фазы колебаний, приходящих от опорного элемента, вы­читаются из фаз во всех элементах разрешения каждого дальностного портре­та.

Однако алгоритм доминирующего отражателя (АДО), работающий по опорному элементу, не всегда реализуем. По экспериментальным данным для целей больших размеров [40] при разрешающей способности по ради­альной дальности Δr =1м опорный элемент выделяется в 80% случаев, а при разрешающей способности Δr =3м только в 25% случаев. Представляет поэтому интерес фазирование согласно алгоритмам по совокупности отражате­лей (АСО).

Работа одного из таких алгоритмов (АСО 1) предусматривает последова­тельную оценку сдвига фаз между (v-1)-м и v-мдальностными портретами

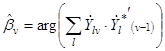. (3.14)

Значение 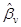используется для фазовой коррекции v-го дальностного пор­трета. Его комплексные отсчеты умножаются для этого на фазовый множи­тель ехр(-j 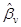), так что

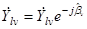. (3.15)

Начальная фаза первого портрета β₁ несущественна и полагается извест­ной и равной нулю. Согласно [41] близкий алгоритм использовался компа­нией Hughes (в [41] он не приводится).

Возможно привлечение фазовой информации не только двух, но и трех (и более) соседних портретов. Для реализации подобного (3.14) алго­ритма АСО 2

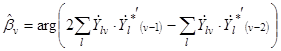(3.16)

требуется, чтобы были известны начальные фазы двух первых дальностных пор­третов. Как и в случае АСО 1, значение фазы β₁ можно принять разным ну­лю, а значение фазы β₂ может быть устранено использованием АСО 1. Синтез алгоритмов АСО 1, АСО 2 и других им подобных производится в предпо­ложении достаточно большого отношения сигнал/шум, позволяющего ис­пользовать максимально правдоподобные оценки фаз 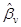в алгоритме оптимальной обработки пачки 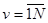ДП (приложение 1, формула П.3) и приближенное равенство величины 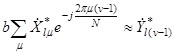. При этом 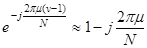(величина 2π/N считается малой).

Применение описанных выше алгоритмов АДО,АСО 1 и АСО 2 иллю­стрируется результатами математического и гидроакустического моделирования получения радиоизображений самолетов.

На рис. 3.3, а, б, в, г приведены дальностно-азимутальные портреты самоле­тов на ракурсе 89° по результатам математического моделирования. Имитиро­валась работа РЛС с длиной волны λ=3 см и широкополосным ЛЧМ-сигналом с эффективной шириной спектра 80 МГц, что обеспечивало разрешаю­щую способность по радиальной дальности 2 м. Модель цели равномерно вра­щалась вокруг центра масс. Суммарный угол поворота примерно 0,4° обеспе­чивал равенство разрешающей способности по поперечной линии визирования дальности и по радиальной дальности. Полученное в этих условиях идеальное (при отсутствии флюктуаций начальных фаз в ДП) радиоизображение приве­дено на рис. 3.3, а. Наличие флюктуаций начальных фаз ДП препятствует восстановлению радиоизображения цели (рис. 3.3, 6). Применение в этом слу­чае АДО и АСО 1 позволяет восстановить изображение цели (рис. 3.3, в и г).

Аналогичные дальностно-азимутальные портреты модели самолета били получены путем гидроакустического моделирования (рис. 3.4, а, б, в,). В отличие от рис. 3.3 на рис. 3.4, г изображение соответствует использованию АСО 2.

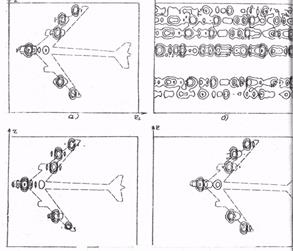
Рис.3.3. Дальностно-азимутальные портреты самолета в отсутствие его рысканий (по результатам математического моделирования); а – в отсутствие флюктуаций начальных фаз дальностных портретов; б – при наличии нескомпенсированных флюктуаций начальных фаз ДП; в – при компенсации флюктуа­цийначальных фаз ДП согласно алгоритму АДО; г – при компенсации флюктуацийначальных фаз ДП согласно алгоритму АСО 1

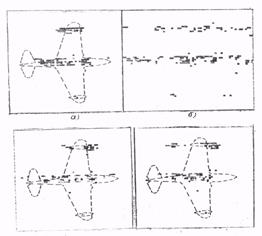
Рис. 3.4. Дальностно-азимутальные портреты самолета в отсутствие его ры­сканий (по результатам гидроакустического моделирования): а – в отсутствие флюктуаций начальных фаз ДП; б – при наличии нескомпенсированных флюк­туаций начальных фаз ДП; в – при компенсации флюктуаций начальных фаз ДП согласно алгоритму АДО; г – при компенсации флюктуаций начальных фаз ДП согласно алгоритму АСО 2

3.8. ПРИНЦИПЫ АДАПТАЦИИ К РЫСКАНИЯМ ЦЕЛИ

Рыскания по углам курса, крена и тангажа приводят к случайному харак­теру величины и направления вектора угловой скорости вращения цели относительно радиолокатора. В результате появляется случайная составляющая амплитудно-фазового распределения на синтезируемой апертуре, вызывающая ее расфокусирование. Так как время когерентности эхо-сигнала от рыскающей цели (даже при использовании алгоритмов АДО или АСО) не превышает 0,3…1 с [40], то и время синтезирования апертуры не может превышать ука­занного времени. Получение двумерных портретов аэродинамических целей на дальностях свыше 30 км становится в этих условиях сложной задачей.

Увеличение дальности получения двумерных изображений возможно при использовании следующих мер: а) применение методов сверхразрешения, позволяющих повысить угловое разрешение для апертуры ограниченного раз­мера; 6) сочетание когерентной обработки сигналов на интервале когерентно­сти с некогерентной на всем интервале времени наблюдения; в) компенса­ция амплитудно-фазовых флюктуаций в элементах ДП, возникающих за счет рысканий.

Рассмотрим каждое направление (разд. 3.8.1 - 3.8.3) в отдельности.

3.8.1. ПРИМЕНЕНИЕ МЕТОДОВ УГЛОВОГО СВЕРХРАЗРЕШЕНИЯ

Угловое сверхразрешение основано на методах обработки сигналов, отли­чающихся от согласованной обработки, обеспечиваемой с помощью ДПФ. Первые работы по угловому сверхразрешению, проводившиеся на Украине [69], явились основой для развития техники корреляционной автокомпенсации помех [125]. Сверхразрешение дает возможность получать радиоизображения аэродинамических целей требуемого качества при инверсном синтезировании апертур меньшего, чем при использовании ДПФ, размера [123].

Сверхразрешение связано в общем случае с известными потерями энер­гии. Коэффициент использования энергии k (относительно энергии, необхо­димой для обнаружения сигнала при одном интенсивном "мешающем" отра­жателе) определяется [69, 70] выражением

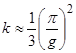, (3.17)

При отношении сигнал/шум 20 дБ применение методов сверхразрешения может дать выигрыш в разрешающей способности до 4 раз. Это позволяет увеличить дальность получения радиоизображения до 4 раз при том же времени когерентности сигнала.

В настоящее время в качестве алгоритмов углового сверхразрешения ис­пользуют цифровые алгоритмы нелинейного спектрального анализа. В рас­сматриваемом случае это естественно, поскольку разрешение по углу сводится к разрешению по доплеровской частоте. Для этих алгоритмов характерен от­каз от простейших расчетов периодограмм временных рядов элементов ДП из-за свойственных им недостатков. Нелинейные методы спектрального анали­за связаны с экстраполяцией имеющихся данных (автокорреляционных функ­ций) за пределы окна наблюдения на основе априорных данных, имеющихся во многих случаях. Для оценки спектра мощности используются нелинейные функции оценочной корреляционной матрицы 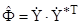. Здесь 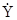- N -элементный вектор анализируемых комплексных амплитуд отсчетов временного ряда. 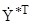- его комплексно-сопряженное транспонированное значение. В роли дискретных спектральных оценок наиболее часто используются функции вида [70]

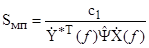; (3.18)

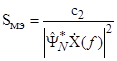. (3.19)

Здесь 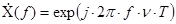, v =0,(N - 1) - опорный N-элементный век­тор дискретизированных по времени (t - vT) гармонических колебаний раз­личных частот f, 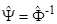- оценка матрицы NхN, обратной корреляционной; 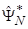- оценка N-й строки матрицы 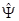; c₁,с₂ - нормирующие коэффициенты.

Оценки вида (3.18) называют в литературе спектральными оценками максимального правдоподобия (оценками МП-спектра по Кейпону), оценки вида (3.19) называют спектральными оценками максимальной энтропии (оценками МЭ-спектра по Бергу) [70, 126, 127]. МЭ-спектр характеризуется более вы­соким разрешением, но и большим смещением оценок, чем МП-спектр.

Пример получения дальностно-азимутального портрета модели рыскающего самолета при большом времени наблюдения представлен на рис. 3.5, а. Пор­трет (рис. 3.5,б) получен при использовании МП-метода с уменьшениемвремени наблюдения в 8 раз. Энергетические потери, обусловленные сокращени­ем времени наблюдения и использованием сверхразрешения, скомпенсированы увеличением отношения сигнал/шум на один дальностный портрет.

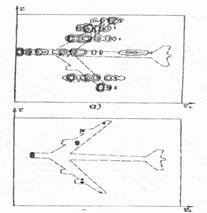
Рис. 3.5. Дальностно-азимутальные портреты самолета при наличии его рысканий (по результатам математического моделирования): а – без применения мер по устранению влияния рысканий б – с использованием углового сверхразрешения

3.8.2. СОЧЕТАНИЕ КОГЕРЕНТНОЙ ОБРАБОТКИ С НЕКОГЕРЕНТНОЙ

Сочетание когерентной обработки с некогерентной возможно по крайней мере, в двух вариантах.

Во-первых, при разрешении блестящих точек цели по радиальной дальности можно получить двумерное изображение при синтезировании небольших апертур, соответствующих значениям времени когерентности Т_к. Разрешение элементов цели поперечное линии визирования, заменяется в этом случае измерением их координат, поперечных линии визирования. Для осуществления же точных измерений достаточно ограничиться апертурами небольшого разме­ра, повышая точность измерения за счет накопления оценок [71]. Если все отражающие элементы цели не удается разрешить по радиальной дальности, то получаемый таким образом двумерный портрет будет иметь значительные искажения, т.к. в каждом разрешаемом по радиальной дальности элементе не может содержаться более одной точки.

Во-вторых, при отсутствии разрешения всех элементов цели по радиальной дальности можно измерить координаты фазовых центров в каждом элементе дальности, синтезируя Т_н / Т_к ограниченных апертур за время наблюдения Т_н. Оценки поперечного размера цели определяются по ширине спектра мощности амплитудных флюктуаций эхо-сигналов на интервале времени Т_и. Располагая знаниями поперечного размера цели в каждом разрешаемом по радиальной дальности элементе и положением его центра, можно построить двумерное квазиизображение цели [71]. Двумерный портрет рыскающей цели, полученный этим способом, представлен на рис. 3.6.

3.8.3. КОМПЕНСАЦИЯ АМПЛИТУДНО-ФАЗОВЫХ ФЛЮКТУАЦИЙ, ОБУСЛОВЛЕННЫХ

РЫСКАНИЯМИ ЦЕЛИ, В ЭЛЕМЕНТАХ ДАЛЬНОСТНЫХ ПОРТРЕТОВ

Случайные изменения ориентации цели (рыскания) за время накопления отраженных сигналов приводят к возникновению: а) флюктуаций фазы в элементах дальности, содержащих одну блестящую точку; б) амплитудно-фазовых флюктуаций в элементах дальности, содержащих несколько блестящих точек.

Случайного амплитудно-фазового (фазового) распределения не возникает, если дальностные портреты цели фиксируются при ее разворотах на один и тот же угол. Для устранения влияния рысканий цели возможно: а) пол­учать избыточные выборки эхо-сигналов, увеличив частоту повторений в не­сколько раз; б) оценить законы рысканий цели; в) зная эти законы, выби­рать для построения двумерного изображения дальностные портреты, соответствующие последовательным разворотам цели на одинаковые утлы. По избыточ­ной выборке можно получить несколько наборов данных для получения двумерных изображений, которые потом можно некогерентно суммировать.

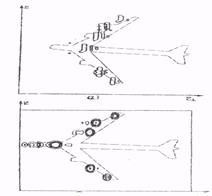
Рис.3.6. Дальностно-азимутильные портреты самолета при наличии его рысканий (по результатам математического моделировании): а - при сочетании когерентной и некогерентной обработки: б- при компенсации ал