Элементы алгоритмов связанные с получением дальностных портретов целей

Рассматриваемые элементы относятся ко второй группе слагаемых (2.13) - (2.14). В пренебрежении флюктуациями формы портретов ожидаемый сиг­нал соответствует модели пачки импульсов с неизвестными их начальными фазами 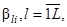с общим неизвестным амплитудным множителем b. Счи­тая для упрощения рассмотрения, что комплексные отсчеты 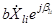прини­маемого сигнала снимаются с выхода согласованного фильтра, получим

.

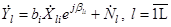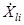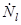Здесь и - комплексные отсчеты сигнала и шума соответствен­но. Комплексные отсчеты сигнала нормированы так, что

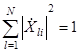
Составляющие 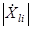образуют i-й эталонный ДП. При цифровой обра­ботке сигнала комплексные отсчеты 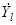принимаемого сигнала характеризуются их квадратурными составляющими.

Для гауссовской помехи с дисперсиями квадратурных составляющих 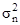логарифмы плотностей вероятности для случаев отсутствия, и наличия сигнала 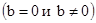, а также логарифм отношения правдоподобия имеют вид

;

;

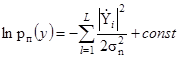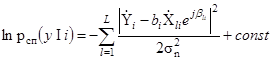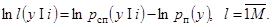
При асимптотически высоком отношении сигнал-шум можно оценить слу­чайные параметры β_li и b_i по максимуму правдоподобия, с тем, чтобы иск­лючить их из выражений 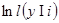. Оценки параметров 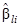в частности, выбираются из условия 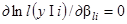при 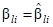после замены квад­рата модуля входящей в нею комплексной величины ее произведением на комплексно-сопряженную. Оценки 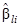имеют вид

.

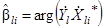Аналогично находятся оценки амплитудного множителя

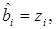
где z_i - приводившаяся ухе в разделе 1.4 корреляционная сумма

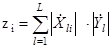. (2.19)

После подстановки оценок начальных фаз и общего амплитудного множителя логарифм оценочного значения отношения правдоподобия, входящий как некий v -6 элемент аддитивного выражения (2.14), принимает вид

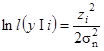. (2.20)

Входящая в (2.20) корреляционная сумма пропорциональна коэффициенту корреляции принимаемого портрета с ожидаемым (эталонным)

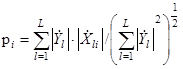
В отсутствие точного совмещения портрета и эталона такое совмещение проводят по максимуму корреляции.

Один из способов учета флюктуаций формы портретов состоит во введе­нии для каждого класса нескольких подклассов с различающимися эталонны­ми портретами. Решение по частному признаку "протяженность цели" прини­мается тогда в пользу класса, подкласс которого дает наибольшую корреля­ционную сумму (2.19) при эталонах подклассов, выбранных для установлен­ного заранее сектора ракурсов.