НЕЙРОКОМПЬЮТЕРНЫЕ АЛГОРИТМЫ
Относятся к одноэтапным алгоритмам с условной оптимизацией. Условием является частично заданная их структура. Структура задается из аналогий с гипотетическими биологическими нейросистемами (нейросетями) Экспериментальные достижения в этой области часто трактуют как проявления искусственного интеллекта. Обучение (адаптация) нейрокомпьютерных систем (алгоритмов) проводится на основе предъявления большого числа случайных обучающих образцов процессов или объектов известных классов. Статистические закономерности последних заранее, как правило, не анализируют, а автоматически учитывают в процессе обучения. Пространство входных сигналов 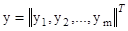 разделяется в результате нелинейными границами на области, соответствующие различным классам. Ценою универсализации структур нейросистем является увеличение вычислительных затрат, компенсируемое развитием вычислительной техники [52 – 56].
разделяется в результате нелинейными границами на области, соответствующие различным классам. Ценою универсализации структур нейросистем является увеличение вычислительных затрат, компенсируемое развитием вычислительной техники [52 – 56].
2.4.1. ПРИНЦИПЫ ПОСТРОЕНИЯ И СТРУКТУРЫ И ЕЙРО КОМПЬЮТЕРНЫХ АЛГОРИТМОВ
Искусственные нейроныкак элементы искусственных нейросистем описывают чаще всего, сочетанием нелинейных и линейных операций вида
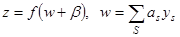 . (2.31)
. (2.31)
Поступающие значения ys (s=1,2,…,m) подаются при этом в различных линейных комбинациях на т элементов "скрытого" слоя нейронов или, иначе, слоя "внутреннего представления", в котором эти комбинации претерпевают "мягкое² ограничение дифференцируемыми монотонно нарастающими функциями 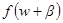 . В качестве функций
. В качестве функций 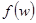 вводят, например, функции вида
вводят, например, функции вида 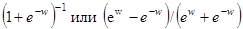 , изменяющиеся соответственно от 0 до 1 и от -1 до 1 при изменении w от
, изменяющиеся соответственно от 0 до 1 и от -1 до 1 при изменении w от 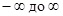 . Параметр b может сдвигатьхарактеристику
. Параметр b может сдвигатьхарактеристику 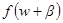 пооси w – менять "мягкий" порог.
пооси w – менять "мягкий" порог.
Выходные данные слоя внутреннего представления подаются, в свою очередь, на п - элементов выходного слоя нейронов, причем также в различных линейных комбинациях и с последующим "мягким" (или "жестким") ограничением. Описанную трехслойную нейроструктуру (рис. 2.1,а) называют персептроном Розенблатта (perception – восприятие, понимание, сознание).
Трехслойная структура не является единственно возможной. Возможны, например, персептроны с четырьмя и более слоями. Анализ многослойных, трехслойных в частности, структур может сводиться, однако, к анализу однослойных структур с последовательно следующими т входными элементами N - т "скрытыми" элементами - элементами внутреннего представления п - выходными элементам (рис. 2.1.6). Входная информация в такой структуре перемещается строго вперед обеспечивая классифицированные решения на п - выходных элементах.
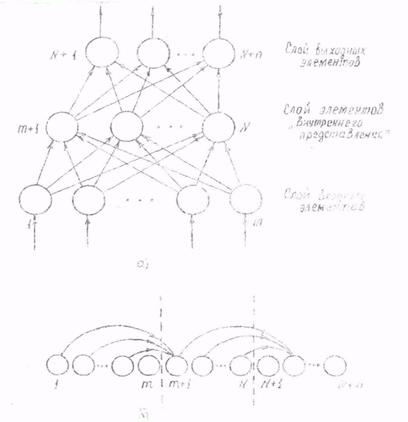
Рис. 2.1. Варианты расположения элементов нейроструктур
Предварительное обучение рассчитано на рациональный выбор весовых коэффициентов а и порогов β на основе возникающих несоответствий выходных отсчетов zвыхi известным zpi для классов обучающих реализаций. Информация о необходимости и характере корректировок должна распространяться в направлении, обратном распространению входной информации - с выхода на вход, в связи с чем говорят о методе обратного распространения.
Возможны разновидности нейросетей: с использованием корреляционных обратных связей; с заменой функций от линейных комбинаций (от линейных форм) квадратичными формами или формами более высокого порядка, что сокращает потребное число нейронных элементов, однако за счет усложнения их структуры.
ВАРИАНТЫ АЛГОРИТМОВ ФУНКЦИОНИРОВАНИЯ И ОБУЧЕНИЯ
Алгоритм функционирования однослойной искусственной нейросети (рис. 2.1.б) обычно имеет вид [55]
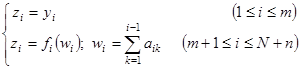 (2.32)
(2.32)
Пороги могут вводиться неодинаковыми β=βi при выборе функций fi(w)=f(w+βi).
В случае трехслойного персептрона (рис. 2.1,а) часть введенных значений aik обращается в нуль. Отсчеты zi, а именно, входные, выходные и "скрытые", принимают вид
 (2.33)
(2.33)
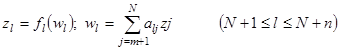 (2.34)
(2.34)
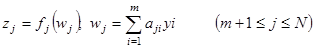 (2.35)
(2.35)
Алгоритмы обучения (адаптации). Вводятся обычно из условия минимизации суммы квадратов невязок выходных отсчетов zl 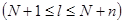 с отсчетами zpl, заранее заданными в процессе предъявления
с отсчетами zpl, заранее заданными в процессе предъявления 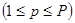 обучающих входных многомерных реализации yi=ypi
обучающих входных многомерных реализации yi=ypi 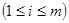 . Задав минимизируемую функцию стоимости потерь аддитивной и квадратичной, можно представить ее в виде
. Задав минимизируемую функцию стоимости потерь аддитивной и квадратичной, можно представить ее в виде
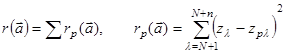 . (2.36)
. (2.36)
Аргументом функций 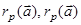 является вектор
является вектор 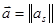 весовых коэффициентов аlj, aji . Переменная суммирования l заменена в (2.36) на λ.
весовых коэффициентов аlj, aji . Переменная суммирования l заменена в (2.36) на λ.
Для минимизации можно использовать численные методы поиска безусловных экстремумов: метод Ньютона, градиентный метод.
При градиентном поиске начальное значение 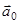 вектора
вектора 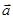 получает последовательные приращения
получает последовательные приращения
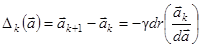 (k=0,1,2,….) (2.37)
(k=0,1,2,….) (2.37)
где 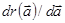 - градиент функции
- градиент функции 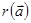 , а γ - постоянный коэффициент.
, а γ - постоянный коэффициент.
Процесс градиентного поиска может осуществляться в ходе последовательного предъявления обучающих реализаций. Предыдущее равенство переходит тогда в
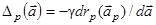 (p=0,1,2,…) (2 .38)
(p=0,1,2,…) (2 .38)
Для составляющих as вектора 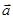 отсюда следует
отсюда следует
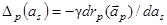
 (2.39)
(2.39)
Если составляющая as относится к выходному слою трехслойного персептрона as=aij 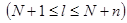 то ненулевую производную по аlj имеет только слагаемое λ=l выражения (2.36). Тогда [56]
то ненулевую производную по аlj имеет только слагаемое λ=l выражения (2.36). Тогда [56]
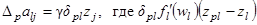 (2.40)
(2.40)
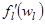 - производная функции fl(w) по ее аргументу.
- производная функции fl(w) по ее аргументу.
Если составляющая as относится к "скрытому" слою as=alv 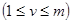 , то в образовании производной по аjv участвуют все слагаемые выражения (2.36)
, то в образовании производной по аjv участвуют все слагаемые выражения (2.36) 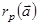 , но лишь одно слагаемое i = v весовой суммы (2.35), причем - только одной j-й суммы
, но лишь одно слагаемое i = v весовой суммы (2.35), причем - только одной j-й суммы 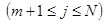 . Тогда
. Тогда
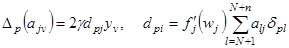 (2 .41)
(2 .41)
Значения δpl вычисляются согласно (2.40).
Для часто используемых функций 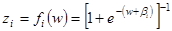 значения
значения
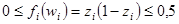 . (2 . 42)
. (2 . 42)
Градиентная процедура настройки неодинаковых порогов β, в выходном и "скрытом" слоях соответственно, определяется выражениями
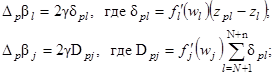 (2.43)
(2.43)
Дата добавления: 2021-02-19; просмотров: 664;











