Потенциальное движение упругой жидкости через недеформируемый пласт

При данном виде течения будем считать k=const, h=const, но

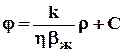. (3.14)

Подобно тому, как в случае однородной несжимаемой жидкости существует линейная зависимость между потенциалом jи давлением р, так в установившимся потоке малосжимаемой жидкости существует линейная зависимость между jи плотностью r. Это означает, что для упругой жидкости зависимость между rкоординатой rвыражается точно теми же формулами, какими выражается зависимость между ри r при однородной несжимаемой жидкости. Чтобы найти зависимость для давления подставим в уравнения, связывающие переменные rи r, значения r,r_к и r_с, определяемые уравнением состояния (2.27) 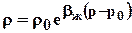. Тогда для плоскорадиального течения имеем

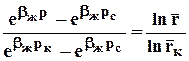. (3.35)

Если взять приближенное линейное уравнение состояния, то придём к тем же зависимостям междур и r, что и при однородной несжимаемой жидкости.

Массовый дебит для упругой жидкости определяется из (3.5) 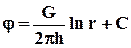при подстановке j из (3.14)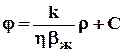

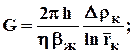(3.36)

Приближенная формула массового дебита получаются при использовании линейного уравнения состояния

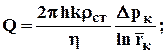(3.36*)

Разделив G на плотность r, найдем объёмный дебит Q, приведённый к тому давлению, которому соответствует плотность r. Так, приводя объёмный дебит к стандартному давлению в 0,1013 МПа , делим G на r_ст . В этом случае формула (3.36) будет совпадать с формулой (3.21), справедливой для несжимаемой жидкости.

Пренебрегать сжимаемостью жидкости в установившемся потоке можно только при условии достаточно малой величины коэффициента b_жи не очень большого перепада давления D р_с=р_к - р_с. В этом случае можно, как для несжимаемой жидкости, считать постоянным вдоль потока не только массовый дебит, но и объёмный. В противном случае вдоль потока: постоянен только массовый дебит; массовая скорость фильтрации изменяется по тому же закону, что скорость фильтрации для несжимаемой жидкости.

Время движения частицы упругой жидкости рассчитывается так же, как и для несжимаемой жидкости.