Течение несжимаемой жидкости в трещиноватом (деформируемом) пласте

Для данных условий r=const , h=const, 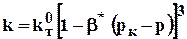и

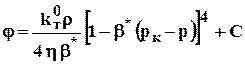. (3.12)

Основные зависимости:

распределение давления

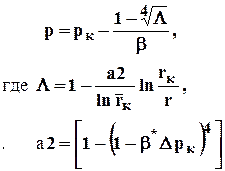(3.29)

градиент давления

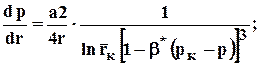(3.30)

объёмный дебит (формула Дюпюи)

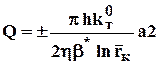, (3.31)

где знаки перед выражением в правой части зависят от того, является ли скважина эксплуатационной или нагнетательной;

скорость фильтрации

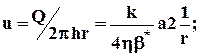(3.32)

При малых депрессиях на пласт из-за малости b^*можно считать, что

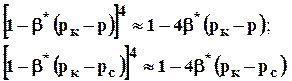
и тогда зависимость для давления (3.29) переходит в вид, аналогичный распределению давления в недеформируемом пласте.

При b^*=0, т.е. для недеформируемого трещиноватого пласта, после раскрытия неопределённости в формуле(3.31) получаем формулу Дюпюи.

Анализ:

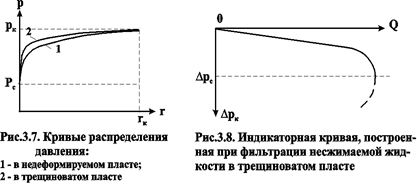
1. В общем случае воронка депрессии для деформируемого пласта более крутая, чем для недеформируемого пористого пласта (рис. 3.7). Указанный характер графиков подтверждает, что в деформируемом трещиноватом пласте, за счет уменьшения раскрытости трещин, при снижении пластового давления возникают дополнительные фильтрационные сопротивления, вызывающие резкое понижение давления на сравнительно небольшом расстоянии от скважины, причем более резко снижается давление в пласте с большим b^*.

2. Из формулы для объёмного дебита (3.31) следует, что индикаторная кривая - парабола четвёртого порядка с координатами вершины:

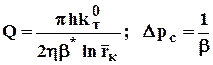. (3.33)

Парабола проходит через начало координат, симметрична относительно оси, параллельной оси дебитов; вторая ветвь смысла не имеет (рис.3.8). Однако, если учесть реальные пластовые условия (полного смыкания трещин не происходит: не учитываются факторы, связанные с изменением характеристик течения из-за изменения раскрытия трещин в направлении потока), то можно говорить только о приближённом выполнении экстремальных условий (3.33).

3. Комплексный параметр b^* можно определить или графоаналитически, или непосредственно из (3.31), взяв по индикаторной кривой два известных значениях дебита Q₁и Q₂при двух значениях депрессии Dр_с1 , Dр_с2 , т.е. из соотношения

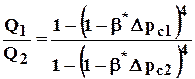. (3.34)

По найденному b^* можно из уравнения (3.31) определить проницаемость k⁰_т.